题目内容
各项均为正数的等比数列 ,
, ,
, ,单调增数列
,单调增数列 的前
的前 项和为
项和为 ,
, ,且
,且 (
( ).
).
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)令 (
( ),求使得
),求使得 的所有
的所有 的值,并说明理由.
的值,并说明理由.
(Ⅲ) 证明 中任意三项不可能构成等差数列.
中任意三项不可能构成等差数列.
 ,
, ,
, ,单调增数列
,单调增数列 的前
的前 项和为
项和为 ,
, ,且
,且 (
( ).
).(Ⅰ)求数列
 、
、 的通项公式;
的通项公式;(Ⅱ)令
 (
( ),求使得
),求使得 的所有
的所有 的值,并说明理由.
的值,并说明理由.(Ⅲ) 证明
 中任意三项不可能构成等差数列.
中任意三项不可能构成等差数列.(Ⅰ) ,
, (Ⅱ)所有
(Ⅱ)所有 的值为1,2,3,4,理由见解析(Ⅲ)证明见解析
的值为1,2,3,4,理由见解析(Ⅲ)证明见解析
 ,
, (Ⅱ)所有
(Ⅱ)所有 的值为1,2,3,4,理由见解析(Ⅲ)证明见解析
的值为1,2,3,4,理由见解析(Ⅲ)证明见解析试题分析:(Ⅰ)设等比数列
 的公比为
的公比为 ,
,∵

 =
= ,
, ,
,
 =4,
=4,∵
 ,∴
,∴ ,∴
,∴ . ……3分
. ……3分∴

∵
 +2 ①
+2 ①当
 时,
时, +2 ②
+2 ②①-②得
 ,即
,即 ,
,∵
 ∴
∴ =3,
=3,∴
 是公差为3的等差数列.
是公差为3的等差数列.当
 时,
时, +2,解得
+2,解得 =1或
=1或 =2,
=2,当
 =1时,
=1时, ,此时
,此时 =7,与
=7,与 矛盾;
矛盾;当
 时
时 ,此时此时
,此时此时 =8=
=8= ,
,∴
 . ……6分
. ……6分(Ⅱ)∵
 ,∴
,∴ =
= ,
,∴
 =2>1,
=2>1, =
= >1,
>1,
 ,
,
 ,
,
 ,
,下面证明当
 时,
时,
事实上,当
 时,
时, =
= <0
<0即
 ,∵
,∵
 , ∴当
, ∴当 时,
时, ,
,故满足条件
 的所有
的所有 的值为1,2,3,4. ……11分
的值为1,2,3,4. ……11分(Ⅲ)假设
 中存在三项
中存在三项 (
( ,
, ∈N*)使
∈N*)使 构成等差数列,
构成等差数列,∴
 ,即
,即 ,∴
,∴ .
.因左边为偶数,右边为奇数,矛盾.
∴假设不成立,故不存在任意三项能构成等差数列. ……16分
点评:等差数列和等比数列是两类最重要的数列,它们的基本量的运算要灵活掌握,另外,探索性问题通常都是先假设成立,再根据题意求解,如果求出符合要求的值就是存在的,如果求不出符合要求的解,就不存在.

练习册系列答案
相关题目
 的等比中项,则
的等比中项,则 的最大值为( )
的最大值为( )



 中,每 行 中 的 三 个 数 成 等 差 数 列,且
中,每 行 中 的 三 个 数 成 等 差 数 列,且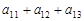 、
、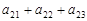 、
、 成等比数列,下列四个判断正确的有 (A )
成等比数列,下列四个判断正确的有 (A ) 必成等比数列 ②第1列
必成等比数列 ②第1列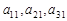 不一定成等比数列
不一定成等比数列 ④若9个数之和等于9,则
④若9个数之和等于9,则
 中,
中, ,则数列
,则数列 的公比为
的公比为 ,前n项和
,前n项和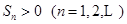 。
。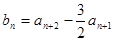 ,记
,记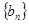 的前n项和为
的前n项和为 ,试比较
,试比较 与
与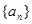 中,有
中,有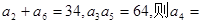
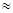 1.921,1.07510
1.921,1.07510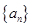 的各项均为正数,且
的各项均为正数,且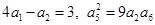 . (1)求数列
. (1)求数列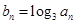 ,求数列
,求数列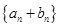 的前
的前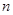 项和
项和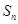 .
.
 是等比数列;
是等比数列;