题目内容
(本小题满分12分)设等比数列 的公比为
的公比为 ,前n项和
,前n项和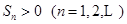 。
。
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)设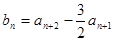 ,记
,记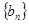 的前n项和为
的前n项和为 ,试比较
,试比较 与
与 的大小。
的大小。
 的公比为
的公比为 ,前n项和
,前n项和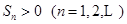 。
。(Ⅰ)求
 的取值范围;
的取值范围;(Ⅱ)设
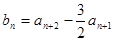 ,记
,记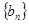 的前n项和为
的前n项和为 ,试比较
,试比较 与
与 的大小。
的大小。(Ⅰ)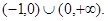 (Ⅱ)当
(Ⅱ)当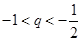 或
或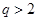 时,
时,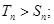
当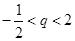 ,
,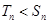 ;当
;当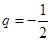 或
或 =2时,
=2时,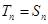
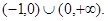 (Ⅱ)当
(Ⅱ)当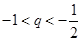 或
或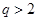 时,
时,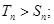
当
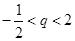 ,
,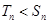 ;当
;当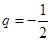 或
或 =2时,
=2时,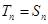
试题分析:(Ⅰ)因为
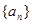 是等比数列,
是等比数列,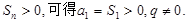
当

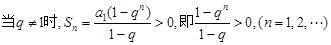
上式等价于不等式组:
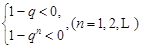 ① 或
① 或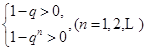 ②
②解①式得q>1;解②,由于n可为奇数、可为偶数,得-1<q<1.
综上,q的取值范围是
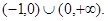 ……6分
……6分(Ⅱ)由
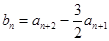 得
得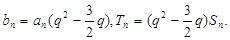
于是
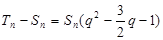
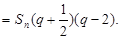
又∵
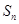 >0且-1<
>0且-1< <0或
<0或 >0
>0当
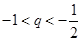 或
或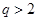 时,
时,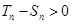 即
即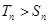
当
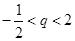 且
且 ≠0时,
≠0时,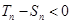 即
即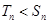
当
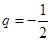 或
或 =2时,
=2时,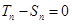 即
即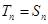 . ……12分
. ……12分点评:应用等比数列的前n项和公式时,要注意公比是否为1,必要时要分情况讨论;比较两个数或两个式子的大小时,常用的方法是作差法或作商法.

练习册系列答案
相关题目
 ,
, ,
, ,单调增数列
,单调增数列 的前
的前 项和为
项和为 ,
, ,且
,且 (
( ).
). (
( 的所有
的所有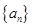 的前
的前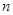 项和为
项和为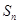 ,满足
,满足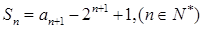 ,且
,且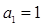 。
。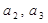 的值;
的值;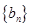 的前
的前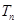 ,且
,且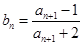 ,证明:对一切正整数
,证明:对一切正整数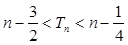
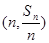 在直线
在直线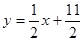 上.数列{bn}满足
上.数列{bn}满足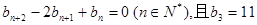 ,前9项和为153.
,前9项和为153.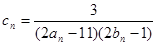 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式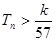 对一切
对一切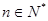 都成立的最大正整数k的值.
都成立的最大正整数k的值.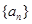 的公比为正数,且
的公比为正数,且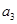
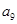 =2
=2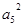 ,
,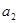 =1,则
=1,则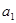 =( )
=( )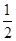
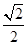
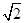
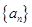 的前
的前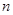 项和为
项和为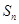 ,
,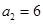 ,
,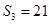 ,求数列
,求数列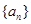 的前
的前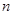 项和为
项和为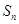 ,若
,若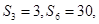 则
则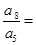 ( )
( ) 8
8