题目内容
(09年崇文区期末文)(14分)
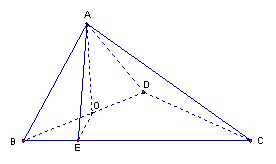
如图,四面体ABCD中,O是BD的中点,ΔABD和ΔBCD均为等边三角形,
AB =2 , AC =![]() .
.
(I)求证:![]() 平面BCD;
平面BCD;
(II)求二面角A-BC- D的大小;

解析:解法一:
证明:连结OC,
![]()
∴![]() . ----------------------------------------------------------------------------------2分
. ----------------------------------------------------------------------------------2分
![]() ,
,![]() ,
,
∴![]() . ------------------------------------------------------4分
. ------------------------------------------------------4分
在![]() 中,
中,![]()
∴![]() 即
即![]() ---------------------------------------------------5分
---------------------------------------------------5分
![]()
∴![]() 平面
平面![]() . ----------------6分
. ----------------6分
(II)过O作![]() ,连结AE,
,连结AE,
![]() ,
,
∴AE在平面BCD上的射影为OE.
∴![]() .
.
∴ ![]() . ---------------------------------10分
. ---------------------------------10分
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴二面角A-BC-D的大小为![]() . -----------------------------------------------14分
. -----------------------------------------------14分
解法二:
(I)同解法一.
(II)解:以O为原点,如图建立空间直角坐标系,
则 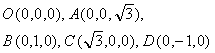 ------------------8分
------------------8分
![]() ,
,
∴![]() . -------------------------------------------------10分
. -------------------------------------------------10分
设平面ABC的法向量![]() ,
,
![]() ,
,![]() ,
,
由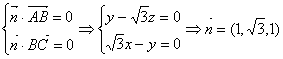 .-----------------------------------12分
.-----------------------------------12分
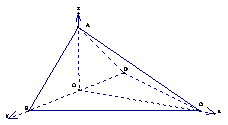 设
设![]() 与
与![]() 夹角为
夹角为![]() ,
,
则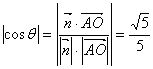 .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案