题目内容
如图，若一个空间几何体的三视图中，直角三角形的直角边长均为1，则该几何体外接球的表面积为（ ）| A、π | B、3π | C、6π | D、12π |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是一个四棱锥，四棱锥的一条侧棱与底面垂直，底面是边长为1的正方形，可以把这个四棱锥看成棱长是1的正方体的一部分，外接球的球心在正方体的对角线上，即在四棱锥的最长的一条棱上，求出球的直径，再求出表面积．
解答：
解：由三视图知，几何体是一个四棱锥，
∵四棱锥的一条侧棱与底面垂直，底面是边长为1的正方形，
∴可以把这个四棱锥看成棱长是1的正方体的一部分，
根据圆和正方体的对称性知．
外接球的球心在正方体的对角线上，即在四棱锥的最长的一条棱上，
∴球的直径是
=
，
∴球的表面积是4×π×(
)2=3π，
故选：B．
∵四棱锥的一条侧棱与底面垂直，底面是边长为1的正方形，
∴可以把这个四棱锥看成棱长是1的正方体的一部分，
根据圆和正方体的对称性知．
外接球的球心在正方体的对角线上，即在四棱锥的最长的一条棱上，
∴球的直径是
| 12+12+12 |
| 3 |
∴球的表面积是4×π×(
| ||
| 2 |
故选：B．
点评：本题考查由三视图求几何体的体积，考查由三视图还原几何体的直观图，考查四棱锥与正方体之间的关系，考查四棱锥的外接球与正方体的关系，本题是一个综合题目．
练习册系列答案
相关题目
“x=-1”是“x2=1”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
如图所示的数阵叫“莱布尼兹调和三角形”，他们是由整数的倒数组成的，第n行有n个数且两端的数均为已知全集A={0，2，4，6}，集合B={2，4，5，6}，则A∩B等于（ ）
| A、{0，2，4，6，} |
| B、{2，4，6} |
| C、{0，2，4，5} |
| D、{0，5} |
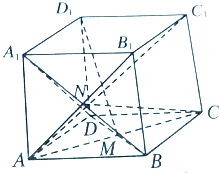如图，在正方形ABCD-A1B1C1D1中，M，N分别为正方形ABCD和AA1B1B的重心．