题目内容
已知正项数列
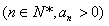 的前n项和
的前n项和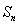 满足:
满足: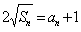 ;设
;设 ,求数列
,求数列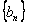 的前n项和的最大值。
的前n项和的最大值。

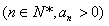 的前n项和
的前n项和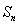 满足:
满足: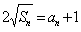 ;设
;设 ,求数列
,求数列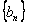 的前n项和的最大值。
的前n项和的最大值。 解:当n=1时, ,所以
,所以 ,即
,即 ,
,
∴ ;
;
当 时,由
时,由 ,得
,得 , ①
, ①
∴ , ②
, ②
两式相减,得 ,
,
整理,得 ,
,
∵ ,
,
∴ ,
,
∴ ,
,
∴ 是以1为首项,以2为公差的等差数列,即
是以1为首项,以2为公差的等差数列,即 ,
,
∴ ,
, ,
,
∴ ,
,
又 ,
,
∴ 是等差数列,且
是等差数列,且 ,公差d=-4,
,公差d=-4,
∴ ,
,
∴当 时,
时, 取最大值,但n∈N*,
取最大值,但n∈N*,
∴当n=10时, 最大,
最大,
最大值为 。
。
 ,所以
,所以 ,即
,即 ,
,∴
 ;
;当
 时,由
时,由 ,得
,得 , ①
, ①∴
 , ②
, ②两式相减,得
 ,
,整理,得
 ,
,∵
 ,
,∴
 ,
,∴
 ,
,∴
 是以1为首项,以2为公差的等差数列,即
是以1为首项,以2为公差的等差数列,即 ,
,∴
 ,
, ,
,∴
 ,
,又
 ,
,∴
 是等差数列,且
是等差数列,且 ,公差d=-4,
,公差d=-4,∴
 ,
,∴当
 时,
时, 取最大值,但n∈N*,
取最大值,但n∈N*,∴当n=10时,
 最大,
最大,最大值为
 。
。
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 的前n项和
的前n项和 满足:
满足: ,
, 和前n项和
和前n项和 的前n项和
的前n项和 ;
; 对任意的
对任意的 ,
, 都成立.
都成立.
 ,然后得到
,然后得到
 得到结论
得到结论 利用裂项求和的思想得到结论。
利用裂项求和的思想得到结论。


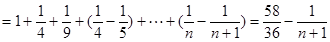
 ∴
∴  ∴
∴
 ∴数列
∴数列 …………………4分
…………………4分 …………………5分
…………………5分  …………………6分
…………………6分
 …………………9分
…………………9分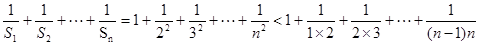
 …………………12分
…………………12分
 的前n项和满足
的前n项和满足
 是数列
是数列 的前n项的和,求证:
的前n项的和,求证: