题目内容
11.已知数列{an}为等比数列,且a2013+a2015=${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx,则a2014(a2012+2a2014+a2016)的值为4π2.分析 ${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx,表示半圆:$y=\sqrt{4-{x}^{2}}$(0≤x≤2)的面积,可得${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx=2π.再利用等比数列的性质即可得出.
解答 解:∵${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx,表示半圆:$y=\sqrt{4-{x}^{2}}$(0≤x≤2)的面积,∴${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx=2π.
∴a2013+a2015=2π,
则a2014(a2012+2a2014+a2016)=${a}_{2013}^{2}$+$2{a}_{2014}^{2}$+${a}_{2015}^{2}$=$({a}_{2013}+{a}_{2015})^{2}$=4π2.
故答案为:4π2.
点评 本题考查了微积分基本定理、等比数列的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.函数f(x)是奇函数,且在(0,+∞)内是单调递增函数,若f(3)=0,则不等式xf(x)<0的解集是( )
| A. | (-3,0)∪(3,+∞) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(0,3) |
6.若变量x,y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y+1≥0}\\{3x-y-1≤0}\end{array}\right.$,则z=x-y的最大值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
20.已知命题p:?x∈(0,+∞),x2≥x-1,则命题p的否定形式是( )
| A. | ¬p:?x0∈(0,+∞),x02≥x0-1 | B. | ¬p:?x0∈(-∞,+0),x02≥x0-1 | ||
| C. | ¬p:?x0∈(0,+∞),x02<x0-1 | D. | ¬p:?x0∈(-∞,+0),x02<x0-1 |
 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.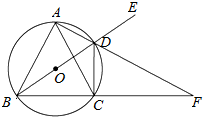 如图所示,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC的延长线于F,DE是BD的延长线,连接CD.
如图所示,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC的延长线于F,DE是BD的延长线,连接CD.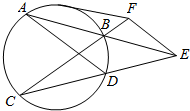 如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证:
如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证: