题目内容
19．函数f（x）是奇函数，且在（0，+∞）内是单调递增函数，若f（3）=0，则不等式xf（x）＜0的解集是（ ）| A． | （-3，0）∪（3，+∞） | B． | （-∞，-3）∪（0，3） | C． | （-∞，-3）∪（3，+∞） | D． | （-3，0）∪（0，3） |
分析 易判断f（x）在（-∞，0）上的单调性及f（x）图象所过特殊点，作出f（x）的草图，根据图象可解不等式．
解答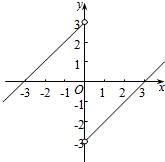 
解：∵f（x）在R上是奇函数，且f（x）在（0，+∞）上是增函数，
∴f（x）在（-∞，0）上也是增函数，
由f（3）=0，得f（-3）=-f（3）=0，
即f（-3）=0，
作出f（x）的草图，如图所示：
由图象，得xf（x）＜0?$\left\{\begin{array}{l}{x＞0}\\{f（x）＜0}\end{array}\right.$或$\left\{\begin{array}{l}{x＜0}\\{f（x）＞0}\end{array}\right.$，
解得0＜x＜3或-3＜x＜0，
∴xf（x）＜0的解集为：（-3，0）∪（0，3），
故选：D．
点评 本题考查函数奇偶性、单调性的综合应用，考查数形结合思想，灵活作出函数的草图是解题关键．
练习册系列答案
相关题目
9．已知F1，F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且∠F1PF2=$\frac{π}{3}$，记椭圆和双曲线的离心率分别为e1，e2，则$\frac{1}{{e}_{1}{e}_{2}}$的最大值为（ ）
| A． | 3 | B． | $\frac{4\sqrt{3}}{3}$ | C． | 2 | D． | $\frac{2\sqrt{3}}{3}$ |
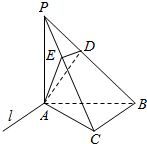如图，在三棱锥P-ABC中，PA⊥底面ABC，PA=AB，∠ABC=60°，∠BCA=90°，点D，E分别在棱PB，PC上，且DE∥BC．平面ADE∩平面ABC=l．
4．集合A={（x，y）|y=|x|}，集合B={（x，y）|y＞0，x∈R}，则下列说法正确的是（ ）
| A． | A⊆B | B． | B⊆A | ||
| C． | A∩B=∅ | D． | 集合A、B间没有包含关系 |