题目内容
1.已知偶函数f(x)在区间[0,+∞)上单调递增,则满足$f(3x-1)<f(\frac{1}{3})$的x的取值范围是($\frac{2}{9}$,$\frac{4}{9}$).分析 利用函数的奇偶性的性质将f(3x-1)<f($\frac{1}{3}$)转化为f(|3x-1|)<f($\frac{1}{3}$)然后利用函数的单调性解不等式即可..
解答 解:∵函数f(x)是偶函数,
∴f(3x-1)<f($\frac{1}{3}$)等价为f(|3x-1|)<f($\frac{1}{3}$),
∵f(x)在区间[0,+∞)上单调递增,
∴|3x-1|<$\frac{1}{3}$,即-$\frac{1}{3}$<3x-1<$\frac{1}{3}$,解得$\frac{2}{9}$<x<$\frac{4}{9}$,
∴x的取值范围是($\frac{2}{9}$,$\frac{4}{9}$).
故答案为:($\frac{2}{9}$,$\frac{4}{9}$).
点评 本题主要考查函数奇偶性的应用,利用函数是偶函数将不等式转化为f(|3x-1|)<f($\frac{1}{3}$)是解决本题的关键.

练习册系列答案
相关题目
13.函数f(x)=2x3+5$\sqrt{2{x^3}-1}$的最小值是( )
| A. | -3? | B. | 1 | C. | $-\frac{21}{4}$? | D. | 7 |
10.下面几种推理过程是演绎推理的是( )
| A. | 两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° | |
| B. | 由平面三角形的性质,推测空间四面体的性质 | |
| C. | 某校高三共有10个班,1班有51人,2班有53人,三班有52人,由此推测各班都超过50人 | |
| D. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n≥2),计算a2、a3,a4,由此猜测通项an |
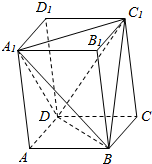 已知四棱锥ABCD-A1B1C1D1的底面是边长为2的正方形,侧棱AA1⊥底面ABCD,若得二面角A1-BD-C1的大小为60°,求四棱柱ABCD-A1B1C1D1的体积.
已知四棱锥ABCD-A1B1C1D1的底面是边长为2的正方形,侧棱AA1⊥底面ABCD,若得二面角A1-BD-C1的大小为60°,求四棱柱ABCD-A1B1C1D1的体积.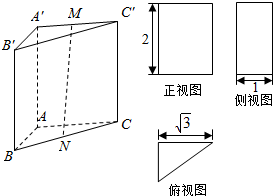 已知一个三棱柱ABC-A′B′C′的三视图由一个直角三角形和两个矩形组成,如图若M,N分别是A′C′,BC的中点.
已知一个三棱柱ABC-A′B′C′的三视图由一个直角三角形和两个矩形组成,如图若M,N分别是A′C′,BC的中点.