题目内容
 如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,
如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,| 5 |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.S△ABC=S△ABP+S△APC=
?x?3+
?y?
=
(3x+
y),S△ABC=
?x?y?
,可得3
x+5y=2xy,利用基本不等式,即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 2 | ||
|
| 5 |
解答:
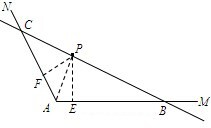 解:过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.
解:过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.
设AB=x,AC=y.
因为P到AM,AN的距离分别为3,
,
即PE=3,PF=
.
由S△ABC=S△ABP+S△APC
=
?x?3+
?y?
=
(3x+
y). ①…(4分)
因为tanα=-2,所以sinα=
.
所以S△ABC=
?x?y?
. ②…(8分)
由①②可得
?x?y?
=
(3x+
y).
即3
x+5y=2xy. ③…(10分)
因为3
x+5y≥2
,所以 2xy≥2
.
解得xy≥15
. …(13分)
当且仅当3
x=5y取“=”,结合③解得x=5,y=3
.
所以S△ABC=
?x?y?
有最小值15.
答:当AB=5km时,该工业园区的面积最小,最小面积为15km2.…(16分)
 解:过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.
解:过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.设AB=x,AC=y.
因为P到AM,AN的距离分别为3,
| 5 |
即PE=3,PF=
| 5 |
由S△ABC=S△ABP+S△APC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
因为tanα=-2,所以sinα=
| 2 | ||
|
所以S△ABC=
| 1 |
| 2 |
| 2 | ||
|
由①②可得
| 1 |
| 2 |
| 2 | ||
|
| 1 |
| 2 |
| 5 |
即3
| 5 |
因为3
| 5 |
15
|
15
|
解得xy≥15
| 5 |
当且仅当3
| 5 |
| 5 |
所以S△ABC=
| 1 |
| 2 |
| 2 | ||
|
答:当AB=5km时,该工业园区的面积最小,最小面积为15km2.…(16分)
点评:本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,回答下列问题: