题目内容
(1)已知x>-1,n∈N*,求证:(1+x)n≥1+nx
(2)已知m>0,n∈N*,ex≥m+nx对于x∈R恒成立,求m与n满足的条件,并求当n=1时m的值.
(3)已知x≤n,n∈N*.求证:n-n(1-
)n•ex≤x2.
(2)已知m>0,n∈N*,ex≥m+nx对于x∈R恒成立,求m与n满足的条件,并求当n=1时m的值.
(3)已知x≤n,n∈N*.求证:n-n(1-
| x |
| n |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)设f(x)=(1+x)n-(1+nx),对函数f(x)求导,得出最小值为f(0)=0;
(2)设M(x0,y0),得出切线方程,由m≤n(1-lnn),m>0,得出n=1时,m是(0,1]上的任意一个值.
(3)由n-n(1-
)n•ex≤x2n-x2≤n(1-
)2•ex当x∈(-∞,-
]∪[
,n]时,n-x2≤0,n(1-
)n•ex≥0不等式成立,从而问题解决.
(2)设M(x0,y0),得出切线方程,由m≤n(1-lnn),m>0,得出n=1时,m是(0,1]上的任意一个值.
(3)由n-n(1-
| x |
| n |
| x |
| n |
| n |
| n |
| x |
| n |
解答:
解 (1)设f(x)=(1+x)n-(1+nx),
则f′(x)=n(1+x)n-1-n,
∴f(x)在(-1,0)递减,在(0,+∞)上递增,
故最小值为f(0)=0得证.
(2)设M(x0,y0),
在M处的切线方程:y=ex0x-x0ex0+ex0
则有:n=ex0且m=-x0ex0+ex0
∴m≤n(1-lnn),m>0,n∈N*
故n=1时,m是(0,1]上的任意一个值.
(3)n-n(1-
)n•ex≤x2n-x2≤n(1-
)2•ex
当x∈(-∞,-
]∪[
,n]时,
n-x2≤0,n(1-
)n•ex≥0不等式成立.
当x∈(0,
)时
n[(1-
)•e
]n≥n[(1-
)(1+
)]nn[(1-
)•e
]n≥n(1-
)n≥n(1-
)≥n-x2.
则f′(x)=n(1+x)n-1-n,
∴f(x)在(-1,0)递减,在(0,+∞)上递增,
故最小值为f(0)=0得证.
(2)设M(x0,y0),
在M处的切线方程:y=ex0x-x0ex0+ex0
则有:n=ex0且m=-x0ex0+ex0
∴m≤n(1-lnn),m>0,n∈N*
故n=1时,m是(0,1]上的任意一个值.
(3)n-n(1-
| x |
| n |
| x |
| n |
当x∈(-∞,-
| n |
| n |
n-x2≤0,n(1-
| x |
| n |
当x∈(0,
| n |
n[(1-
| x |
| n |
| x |
| n |
| x |
| n |
| x |
| n |
| x |
| n |
| x |
| n |
| x2 |
| n2 |
| x2 |
| n |
点评:本题考察了函数的单调性,导数的应用,不等式的证明,是一道综合题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 某市居民2009~2013年货币收入x与购买商品支出Y的统计资料如下表所示:
某市居民2009~2013年货币收入x与购买商品支出Y的统计资料如下表所示:
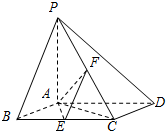 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.