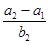题目内容
设曲线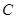 :
: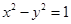 上的点
上的点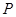 到点
到点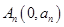 的距离的最小值为
的距离的最小值为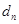 ,若
,若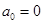 ,
,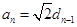 ,
,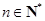
(1)求数列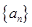 的通项公式;
的通项公式;
(2)求证: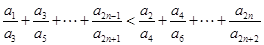 ;
;
(3)是否存在常数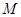 ,使得对
,使得对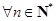 ,都有不等式:
,都有不等式: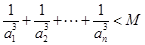 成立?请说明理由.
成立?请说明理由.
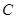 :
: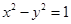 上的点
上的点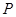 到点
到点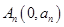 的距离的最小值为
的距离的最小值为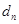 ,若
,若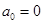 ,
,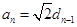 ,
,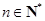
(1)求数列
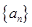 的通项公式;
的通项公式;(2)求证:
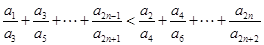 ;
;(3)是否存在常数
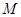 ,使得对
,使得对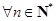 ,都有不等式:
,都有不等式: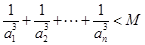 成立?请说明理由.
成立?请说明理由. (1) (2)先证
(2)先证 ,累加即得证.(3)存在常数
,累加即得证.(3)存在常数 ,对
,对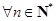 ,都有不等式:
,都有不等式: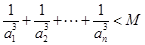 成立.(M取值不唯一)
成立.(M取值不唯一)
 (2)先证
(2)先证 ,累加即得证.(3)存在常数
,累加即得证.(3)存在常数 ,对
,对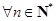 ,都有不等式:
,都有不等式: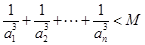 成立.(M取值不唯一)
成立.(M取值不唯一)试题分析:(1)设点
 ,则
,则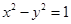 ,∴
,∴ ,
,∵
 , ∴ 当
, ∴ 当 时,
时, 取得最小值
取得最小值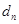 ,且
,且 ,
,又
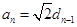 ,∴
,∴ ,即
,即 , 将
, 将 代入
代入 得
得
两边平方,得
 ,又
,又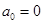 ,
, ,
,∴数列
 是首项为
是首项为 ,公差为
,公差为 的等差数列, ∴
的等差数列, ∴ ,
,∵
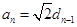
 ,∴
,∴
(2)∵
 ,∴
,∴
∴
 ,∴
,∴ ∴
∴ ,
,∴

将以上
 个不等式相加,得
个不等式相加,得 .
.(Ⅲ)由(1)得
 ,当
,当 时,
时,  ,
,∵
 ,
,∴
 ,
, ∴
 ,
,∴

∴
 .
.∴存在常数
 ,对
,对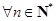 ,都有不等式:
,都有不等式: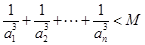 成立.(M取值不唯一)
成立.(M取值不唯一)点评:本题考查数列的通项,考查数列与不等式的综合,考查放缩法的运用,解题的关键是根据目标,适当放缩,难度较大.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
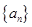 的相邻两项
的相邻两项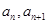 是关于
是关于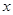 的方程
的方程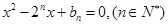 的两根,且
的两根,且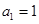 .
.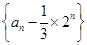 是等比数列;
是等比数列;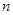 项和
项和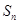 ;
;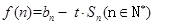 若
若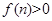 对任意的
对任意的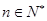 都成立,求
都成立,求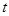 的取值范围。
的取值范围。 中,若a
中,若a - a
- a
 + a
+ a =0(n≥2),则S
=0(n≥2),则S -4n=( )
-4n=( ) 中,
中, ,其前n项的和是
,其前n项的和是 ,则在平面直角坐标系中,直线
,则在平面直角坐标系中,直线 在y轴上的截距为 。
在y轴上的截距为 。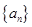 的前
的前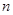 项和记为
项和记为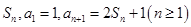
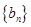 的各项为正,其前
的各项为正,其前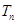 ,且
,且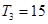 ,又
,又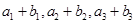 成等比数列,求
成等比数列,求 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 ( )
( )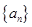 中,
中,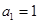 ,
,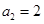 ,且
,且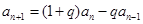
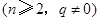 .
.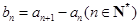 ,求
,求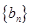 是的通项公式;
是的通项公式;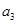 是
是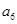 与
与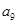 的等差中项,求
的等差中项,求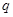 的值,并证明:对任意的
的值,并证明:对任意的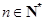 ,
,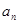 是
是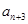 与
与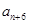 的等差中项.
的等差中项.