题目内容
数列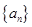 的前
的前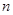 项和记为
项和记为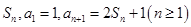
(Ⅰ)求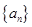 的通项公式;
的通项公式;
(Ⅱ)等差数列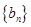 的各项为正,其前
的各项为正,其前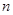 项和为
项和为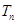 ,且
,且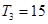 ,又
,又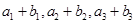 成等比数列,求
成等比数列,求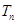
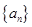 的前
的前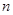 项和记为
项和记为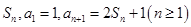
(Ⅰ)求
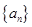 的通项公式;
的通项公式;(Ⅱ)等差数列
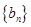 的各项为正,其前
的各项为正,其前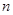 项和为
项和为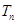 ,且
,且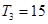 ,又
,又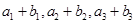 成等比数列,求
成等比数列,求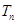
(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
试题分析:(Ⅰ)由
 可得
可得 ,两式相减得
,两式相减得 3分
3分又
 ∴
∴
故
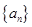 是首项为
是首项为 ,公比为
,公比为 得等比数列
得等比数列∴
 6分
6分(Ⅱ)设
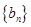 的公差为
的公差为
由
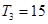 得,可得
得,可得 ,可得
,可得
故可设

又

由题意可得

解得

∵等差数列
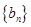 的各项为正,∴
的各项为正,∴
∴
 10分
10分∴
 12分
12分点评:由前n项和
 求通项
求通项 时需分情况讨论:
时需分情况讨论: ,最终看其结果能否合并为一个关系式
,最终看其结果能否合并为一个关系式
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
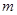 元的一年定期储蓄,若年利率为
元的一年定期储蓄,若年利率为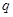 保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )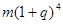 元
元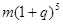 元
元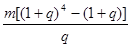 元
元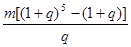 元
元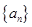 的前
的前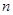 项和为
项和为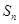 ,
,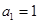 ,
,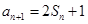
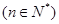 ,等差数列
,等差数列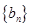 满足
满足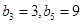 .
.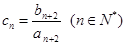 ,求证
,求证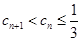 .
.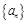 是等差数列,
是等差数列,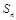 是其前
是其前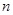 项的和,且
项的和,且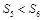 ,
,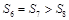 ,则下列结论错误的是
,则下列结论错误的是


 和
和 均为
均为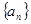 的通项公式为
的通项公式为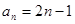 ,数列
,数列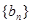 的前n项和为
的前n项和为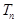 ,且满足
,且满足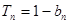
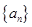 中是否存在使得
中是否存在使得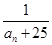 是
是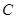 :
: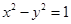 上的点
上的点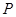 到点
到点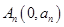 的距离的最小值为
的距离的最小值为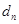 ,若
,若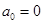 ,
,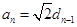 ,
,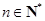
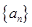 的通项公式;
的通项公式;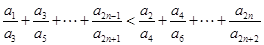 ;
;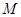 ,使得对
,使得对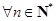 ,都有不等式:
,都有不等式: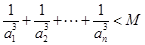 成立?请说明理由.
成立?请说明理由. 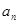 }中,
}中,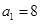 ,
,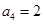 ,且满足
,且满足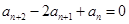
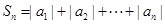 ,求
,求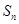 .
.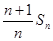
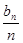 的最小值.
的最小值.