题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与平面ABCD所成的角依次是45°和arctan
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与平面ABCD所成的角依次是45°和arctan| 1 |
| 2 |
(1)求直线EC与平面PAD所成的角(结果用反三角函数值表示);
(2)求三棱锥P-AFD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:计算题,空间向量及应用
分析:以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系,标点,空间向量,通过向量运算解答.
解答:
解: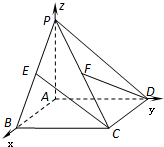 (1)分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系,依题意,AD=4,AB=2,则各点坐标分别是
(1)分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系,依题意,AD=4,AB=2,则各点坐标分别是
A(0,0,0),B(2,0,0),C(2,4,0),D(0,4,0),P(0,0,2);
∴E(1,0,1),F(1,2,1),
=(1,4,-1),
又∵AB⊥平面PAD,
∴平面PAD的法向量为
=
=(2,0,0),
设直线EC与平面PAD所成的角为α,则
sinα=
=
=
,
∴直线EC与平面PAD所成的角为αrcsin
.
(2)由(1)得,
=(1,2,1),
=(0,4,0),
设平面AFD的法向量为
=(x,y,z),点P到平面AFD的距离为d,
由AD?平面AFD,
•
=0得
x+2y+z=0且4y=0,取x=1得
=(1,0,-1),
∴d=
=
=
,
又
=
=
,∴S△AFD=2×
=2
,
∴VP-AFD=
×2
×
=
.
 (1)分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系,依题意,AD=4,AB=2,则各点坐标分别是
(1)分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系,依题意,AD=4,AB=2,则各点坐标分别是A(0,0,0),B(2,0,0),C(2,4,0),D(0,4,0),P(0,0,2);
∴E(1,0,1),F(1,2,1),
| EC |
又∵AB⊥平面PAD,
∴平面PAD的法向量为
| n |
| AB |
设直线EC与平面PAD所成的角为α,则
sinα=
| ||||||||||||||
|
| 2 | ||
2•
|
| ||
| 6 |
∴直线EC与平面PAD所成的角为αrcsin
| ||
| 6 |
(2)由(1)得,
| AF |
| AD |
设平面AFD的法向量为
| n |
由AD?平面AFD,
| AD |
| n |
x+2y+z=0且4y=0,取x=1得
| n |
∴d=
| |||||||||
|
| 2 | ||
|
| 2 |
又
|
|
| 6 |
| 6-4 |
| 2 |
∴VP-AFD=
| 1 |
| 3 |
| 2 |
| 2 |
| 4 |
| 3 |
点评:本题考查了空间中角的求法,及体积的求法,属于难题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目

 已知椭圆E:
已知椭圆E: 四棱锥P-ABCD中,底面ABCD为平行四边形,侧面PBC⊥底面ABCD,E,F分别是PB,AD的中点,已知∠ABC=45°,AB=2,BC=2
四棱锥P-ABCD中,底面ABCD为平行四边形,侧面PBC⊥底面ABCD,E,F分别是PB,AD的中点,已知∠ABC=45°,AB=2,BC=2