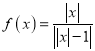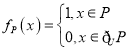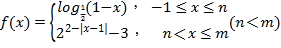题目内容
【题目】(1)![]() 取何值时,方程
取何值时,方程![]() (
(![]() )无解?有一解?有两解?有三解?
)无解?有一解?有两解?有三解?
(2)函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序,研究函数![]() 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在![]() 的草图;
的草图;
【答案】(1)![]() 时,无解;
时,无解;![]() 时,有一解;
时,有一解;![]() 时,有两解;
时,有两解;![]() 时,有三解;
时,有三解;
(2)定义域为![]() ,值域为
,值域为![]() ,周期为
,周期为![]() ,在
,在![]() 为增函数,在
为增函数,在![]() 上为减函数,偶函数;作图见解析
上为减函数,偶函数;作图见解析
【解析】
(1)令函数![]() ,由
,由![]() ,得
,得![]() 的单调性和值域,由此得
的单调性和值域,由此得![]() 的何值范围;
的何值范围;
(2)先研究![]() 的定义域、奇偶性、周期性,再研究函数的单调性、值域,最后画出图形.
的定义域、奇偶性、周期性,再研究函数的单调性、值域,最后画出图形.
(1)令![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
![]() 在
在![]() ,
,![]() 递增,在
递增,在![]() 递减,
递减,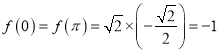 ,
,
![]() ,
,![]() ,
,
综上:![]() 时,无解;
时,无解;![]() 时,有一解;
时,有一解;![]() 时,有两解;
时,有两解;![]() 时,有三解.
时,有三解.
(2)∵![]() ,∴f(x)的定义域为R;
,∴f(x)的定义域为R;
∵![]() ,∴f(x)为偶函数;
,∴f(x)为偶函数;
∵f(x+π)=![]() =
=![]() +
+![]() =f(x),∴f(x)是周期为π的周期函数;
=f(x),∴f(x)是周期为π的周期函数;
当![]() 时,f(x)=
时,f(x)=![]() ,
,
∴当![]() 时,f(x)单调递减;当
时,f(x)单调递减;当![]() 时,
时,
f(x)=![]() ,
,
f(x)单调递增;又∵f(x)是周期为π的偶函数,
∴f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减(k∈Z);
上单调递减(k∈Z);
∵当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .∴f(x)的值域为
.∴f(x)的值域为![]() ;
;
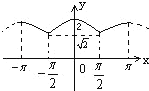
由以上性质可得:f(x)在[﹣π,π]上的图象如图所示:

练习册系列答案
相关题目