题目内容
一个口袋中装有![]() 个红球(
个红球(![]() 且
且![]() )和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(Ⅰ)试用![]() 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率![]() ;
;
(Ⅱ)若![]() ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(Ⅲ)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为![]() .当
.当![]() 取多少时,
取多少时,![]() 最大?
最大?
⑴![]() ,
,![]() ,当
,当![]() 时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大
时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大
解析:
(Ⅰ)一次摸奖从![]() 个球中任选两个,有
个球中任选两个,有![]() 种,
种,
它们等可能,其中两球不同色有![]() 种,………………………2分
种,………………………2分
一次摸奖中奖的概率![]() .………………………4分
.………………………4分
(Ⅱ)若![]() ,一次摸奖中奖的概率
,一次摸奖中奖的概率![]() ,………………………6分
,………………………6分
三次摸奖是独立重复试验,三次摸奖(每次摸奖后放回)恰有一次中奖的概率是
![]() . ………………………8分
. ………………………8分
(Ⅲ)设每次摸奖中奖的概率为![]() ,则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为
,则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为
![]() ,
,![]() , ……………………12分
, ……………………12分
![]() ,知在
,知在![]() 上
上![]() 为增函数,在
为增函数,在![]() 上
上![]() 为减函数,当
为减函数,当![]() 时
时![]() 取得最大值.又
取得最大值.又![]() ,解得
,解得![]() .…………14分
.…………14分
答:当![]() 时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.
时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.
【方法探究】本题是一个在等可能性事件基础上的独立重复试验问题,体现了不同概型的综合.第Ⅲ小题中的函数是三次函数,运用了导数求三次函数的最值.如果学生直接用![]() 代替
代替![]() ,函数将比较烦琐,这时需要运用换元的方法,将
,函数将比较烦琐,这时需要运用换元的方法,将![]() 看成一个整体,再求最值.
看成一个整体,再求最值.

练习册系列答案
相关题目
 个红球(
个红球( 且
且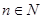 )和
)和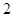 个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.
个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.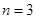 时,设三次摸球中(每次摸球后放回)中奖的次数为
时,设三次摸球中(每次摸球后放回)中奖的次数为 ,求的
,求的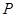 ,当
,当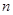 个红球
个红球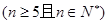 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。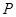 ;
; ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;