题目内容
(本小题满分14分)一个口袋中装有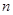 个红球
个红球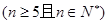 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
(1)试用 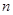 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率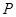 ;
;
(2)若 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(3)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为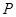 ,当
,当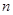 取多少时,
取多少时,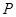 最大?
最大?
【答案】
(1)
(2)
(3)当 时,
时, 最大
最大
【解析】(1) =
= ……………………2分
……………………2分
(2)当 时,
时, =
= ……………………4分
……………………4分
记“三次摸奖(每次摸奖后放回)恰有一次中奖”为事件 ,则
,则 =
=
答:若 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率为
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率为 ……………………6分
……………………6分
(3) =
= ,
, 0<
0< <1
<1 ……………………8分
……………………8分

令 得
得 或
或 (舍去)
……………………11分
(舍去)
……………………11分
当 时,
时, >0;当
>0;当 时,
时, <0;故
<0;故 在
在 处取得最大值,此时
处取得最大值,此时 解得
解得
答:当 时,
时, 最大。
……………………14分
最大。
……………………14分

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)