题目内容
1．在平面直角坐标系xOy中，已知圆C1：（x-4）2+（y-8）2=1，圆C2：（x-6）2+（y+6）2=9．若圆心在x轴上的圆C同时平分圆C1和圆C2的圆周，则圆C的方程是x2+y2=81．分析 由题意，圆C与圆C1和圆C2的公共弦分别为圆C1和圆C2的直径，求出圆心坐标，可得结论．
解答 解：由题意，圆C与圆C1和圆C2的公共弦分别为圆C1和圆C2的直径，
设C（x，0），则（x-4）2+（0-8）2+1=（x-6）2+（0+6）2+9，∴x=0，
∴圆C的方程是x2+y2=81．
故答案为x2+y2=81．
点评 本题考查圆的方程，考查圆与圆的位置关系，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
11．2017年春晚分会场之一是凉山西昌，电视播出后，通过网络对凉山分会场的表演进行了调查．调查分三类人群进行，参加了网络调查的观众们的看法情况如下：
（1）从这三类人群中各选一个人，求恰好有2人认为“非常好”的概率（用比例作为相应概率）；
（2）若在四川人（非凉山）群中按所持态度分层抽样，抽取9人，在这9人中任意选取3人，认为“非常好”的人数记为ξ，求ξ的分布列和数学期望．
| 观众对凉山分会场表演的看法 | 非常好 | 好 |
| 中国人且非四川（人数比例） | $\frac{1}{2}$ | $\frac{1}{2}$ |
| 四川人（非凉山）（人数比例） | $\frac{2}{3}$ | $\frac{1}{3}$ |
| 凉山人（人数比例） | $\frac{3}{4}$ | $\frac{1}{4}$ |
（2）若在四川人（非凉山）群中按所持态度分层抽样，抽取9人，在这9人中任意选取3人，认为“非常好”的人数记为ξ，求ξ的分布列和数学期望．
12．已知集合M={1，3，4}，N={x|x2-4x+3=0}，则M∩N=（ ）
| A． | {3，4} | B． | {1，4} | C． | {1，3} | D． | {3} |
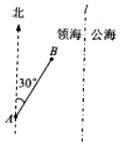一缉私艇巡航至距领海边界线l（一条南北方向的直线）3.8海里的A处，发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑，缉私艇立即追击，已知缉私艇的最大航速是走私船最大航速的3倍，假设缉私艇和走私船均按直线方向以最大航速航行．
13．将函数y=cos（x-$\frac{π}{3}$）的图象上各点横坐标伸长到原来的2倍（纵坐标不变），再向左平移$\frac{π}{6}$个单位，所得函数图象的一条对称轴是（ ）
| A． | x=$\frac{π}{4}$ | B． | x=$\frac{π}{6}$ | C． | x=π | D． | x=$\frac{π}{2}$ |