题目内容
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查500位老人,结果如下:
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?附:
K2=
.
| 男 | 女 | 合计 | |
| 需要 | 40 | 30 | 70 |
| 不需要 | 160 | 270 | 430 |
| 合计 | 200 | 300 | 500 |
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?附:
| P(K2≥k) | 0.50 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)用频率估计概率,从而得到需要志愿者提供帮助的老年人的比例的估计值;
(2)由公式K2=
计算k的值,从而查表即可.
(2)由公式K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
解答:
解:(1)需要志愿者提供帮助的老年人的比例估计为
=14%;
(2)由K2=
代入得,
k=
≈9.967>6.635;
查表得P(K2≥6.635)=0.01;
故有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关.
| 40+30 |
| 500 |
(2)由K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
k=
| 500(40×270-30×160)2 |
| 200×300×430×70 |
查表得P(K2≥6.635)=0.01;
故有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关.
点评:本题考查了独立性检验的应用,属于基础题.

练习册系列答案
相关题目
已知复数z=2+i,则复数z的虚部为( )
| A、2 | B、0 | C、1 | D、i |
在同一坐标系中,函数y=ax+a与y=ax的图象大致是( )
A、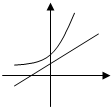 |
B、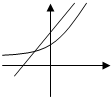 |
C、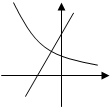 |
D、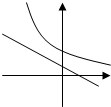 |
已知集合M={x|x2-2x≤0},N={x|
≤0},U=R,则图中阴影部分表示的集合是( )
| 3+x |
| 1-x |

| A、(-∞,0)∪(1,+∞) |
| B、(-∞,-3]∪(2,+∞) |
| C、(-∞,-3)∪(2,+∞) |
| D、(-∞,0]∪[2,+∞) |