题目内容
(1)计算:(
)6-
×(
)
-(-2013)0
(2)已知log73=a,log74=b,用a,b表示log4948.
| 3 | 2 |
| 7 |
| 5 |
| 25 |
| 49 |
| 1 |
| 2 |
(2)已知log73=a,log74=b,用a,b表示log4948.
考点:对数的运算性质,有理数指数幂的化简求值,换底公式的应用
专题:函数的性质及应用
分析:(1)直接利用有理数指数幂的运算法则和运算性质进行求解.
(2)log4948=
log7(3×16),由此能求出结果.
(2)log4948=
| 1 |
| 2 |
解答:
解:(1)(
)6-
×(
)
-(-2013)0
=2
-
×
-1
=4-1-1
=2.
(2)∵log73=a,log74=b,
∴log4948=
log7(3×16)
=
(log73+log716)
=
(log73+2log74)
=
(a+2b).
| 3 | 2 |
| 7 |
| 5 |
| 25 |
| 49 |
| 1 |
| 2 |
=2
| 6 |
| 3 |
| 7 |
| 5 |
| 5 |
| 7 |
=4-1-1
=2.
(2)∵log73=a,log74=b,
∴log4948=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查有理数指数幂的运算法则和运算性质的应用,考查对数的运算法则和运算性质的应用,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=sinxcosx+sinx+cosx取最大值时x的值为( )
A、2kπ+
| ||
B、2kπ-
| ||
C、2kπ+
| ||
D、2kπ-
|
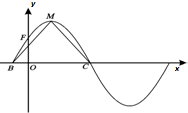 将函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象向右平移
将函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象向右平移 如图,平面α内一椭圆C:
如图,平面α内一椭圆C: