题目内容
18.F是抛物线y2=4x的焦点,P、Q是抛物线上两点,|PF|=2,|QF|=5,则|PQ|=( )| A. | 3$\sqrt{5}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{5}$或$\sqrt{13}$ | D. | 3$\sqrt{5}$或4$\sqrt{3}$ |
分析 根据抛物线的性质将|PF|,|QF|转化为到准线的距离,求出P,Q的坐标,得出答案.
解答 解:抛物线的准线方程为x=-1,
∴|PF|=x1+1=2,|QF|=x2+1=5.
∴x1=1,x2=4.
∴P(1,±2),Q(4,±4),
∴|PQ|=$\sqrt{9+4}$=$\sqrt{13}$或$\sqrt{9+36}$=3$\sqrt{5}$
故选:C.
点评 本题考查了抛物线的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
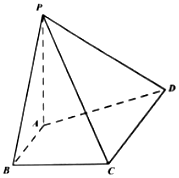 在四菱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
在四菱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.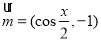 ,
,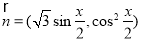 ,函数
,函数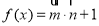 .
.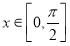 ,
,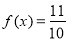 ,求
,求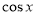 的值;
的值;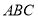 中,角
中,角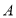 ,
,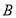 ,
,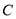 的对边分别是
的对边分别是 ,
,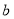 ,
,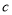 ,且满足
,且满足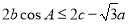 ,求角
,求角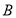 的取值范围.
的取值范围.