题目内容
定义在R上的函数f(x)的导函数为f′(x),且f′(x)>2x,f(1)=2,则不等式f(x)-x2>1的解集为 .
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:构造函数,求函数的导数,利用导数判断函数单调性即可.
解答:
解:设g(x)=f(x)-x2,
则g′(x)=f′(x)-2x,
∵f′(x)>2x,
∴g′(x)=f′(x)-2x>0,
即函数g(x)为增函数,
∵f(1)=2,
∴g(1)=f(1)-1=2-1=1,
则不等式f(x)-x2>1等价为g(x)>g(1),
则x>1,
即不等式的解集为(1,+∞),
故答案为:(1,+∞)
则g′(x)=f′(x)-2x,
∵f′(x)>2x,
∴g′(x)=f′(x)-2x>0,
即函数g(x)为增函数,
∵f(1)=2,
∴g(1)=f(1)-1=2-1=1,
则不等式f(x)-x2>1等价为g(x)>g(1),
则x>1,
即不等式的解集为(1,+∞),
故答案为:(1,+∞)
点评:本题主要考查不等式的求解,根据条件构造函数,利用函数的单调性是解决本题的关键.

练习册系列答案
相关题目
已知PC为球O的直径,A,B是球面上两点,且AB=2
,∠APC=
,∠BPC=
,若球O的体积为
,则棱锥P-ABC的体积为( )
| 2 |
| π |
| 4 |
| π |
| 3 |
| 32π |
| 3 |
A、4
| ||||
B、
| ||||
C、
| ||||
D、
|

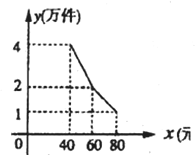 为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.
为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.