题目内容
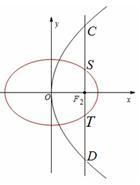
如图,椭圆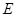 :
: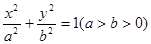 的右焦点
的右焦点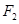 与抛物线
与抛物线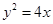 的焦点重合,过
的焦点重合,过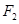 作与
作与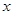 轴垂直的直线
轴垂直的直线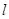 与椭圆交于S、T两点,与抛物线交于C、D两点,且
与椭圆交于S、T两点,与抛物线交于C、D两点,且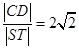 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过点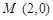 的直线与椭圆
的直线与椭圆 相交于两点
相交于两点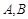 ,设
,设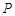 为椭圆
为椭圆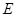 上一点,且满足
上一点,且满足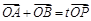 (
(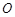 为坐标原点),当
为坐标原点),当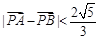 时,求实数
时,求实数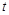 的取值范围.
的取值范围.
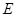 :
: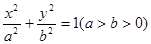 的右焦点
的右焦点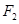 与抛物线
与抛物线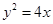 的焦点重合,过
的焦点重合,过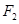 作与
作与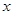 轴垂直的直线
轴垂直的直线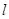 与椭圆交于S、T两点,与抛物线交于C、D两点,且
与椭圆交于S、T两点,与抛物线交于C、D两点,且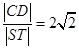 .
.
(Ⅰ)求椭圆
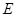 的方程;
的方程;(Ⅱ)若过点
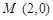 的直线与椭圆
的直线与椭圆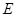 相交于两点
相交于两点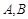 ,设
,设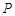 为椭圆
为椭圆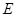 上一点,且满足
上一点,且满足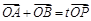 (
(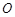 为坐标原点),当
为坐标原点),当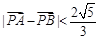 时,求实数
时,求实数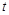 的取值范围.
的取值范围.(Ⅰ)椭圆的方程为 . (Ⅱ)实数
. (Ⅱ)实数 取值范围为
取值范围为 .
.
 . (Ⅱ)实数
. (Ⅱ)实数 取值范围为
取值范围为 .
. 试题分析:(Ⅰ)由抛物线方程,得焦点
 .
.所以椭圆
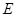 的方程为:
的方程为: .
. 解方程组
 得C(1,2),D(1,-2). 由于抛物线、椭圆都关于x轴对称,
得C(1,2),D(1,-2). 由于抛物线、椭圆都关于x轴对称,∴
 ,
, , ∴
, ∴ . 2分
. 2分因此,
 ,解得
,解得 并推得
并推得 .
. 故椭圆的方程为
 . 4分
. 4分(Ⅱ)由题意知直线
 的斜率存在.
的斜率存在.设
 :
: ,
, ,
, ,
, ,
,由
 得
得 .
. ,
, . 6分
. 6分 ,
, .
.∵
 <
< ,∴
,∴ ,
,∴
 ∴
∴ ,
,∴
 ,∴
,∴ .∴
.∴ , 8分
, 8分∵
 ,∴
,∴ ,
, ,
, .
. ∵点
 在椭圆上,∴
在椭圆上,∴ ,
,∴
 ∴
∴ , 10分
, 10分∴
 或
或 ,
,∴实数
 取值范围为
取值范围为 . 12分
. 12分点评:难题,求椭圆的标准方程,主要运用了抛物线及椭圆的几何性质,建立a,b,c的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)结合向量的坐标运算,确定得到t的函数式,通过确定函数的值域,达到确定实数
 取值范围的目的。利用函数思想解题,是一道好例。
取值范围的目的。利用函数思想解题,是一道好例。
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
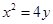 的焦点F的直线
的焦点F的直线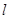 与抛物线相交于A,B两点。
与抛物线相交于A,B两点。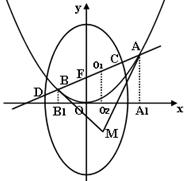
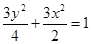 的交点为C、D,是否存在直线
的交点为C、D,是否存在直线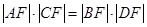 ,若存在,求出直线
,若存在,求出直线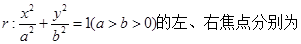
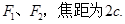 若直线
若直线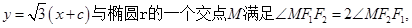 则该椭圆的离心率等于 .
则该椭圆的离心率等于 .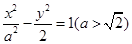 的两条渐近线的夹角为
的两条渐近线的夹角为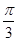 ,则双曲线的离心率为( )
,则双曲线的离心率为( )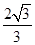
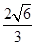
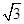
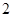
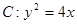 上的不同两点,F为抛物线C的焦点,若
上的不同两点,F为抛物线C的焦点,若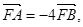 则直线AB的斜率为
则直线AB的斜率为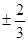 B.
B.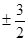 C.
C.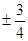 D.
D.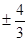
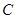 :
: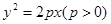 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.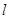 与抛物线
与抛物线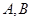 ,若满足
,若满足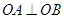 ,证明直线
,证明直线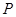 的坐标.
的坐标.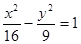 的右顶点为焦点的抛物线的标准方程为 ( )
的右顶点为焦点的抛物线的标准方程为 ( )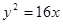
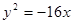

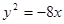
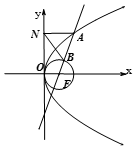
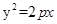 (p>0)的焦点为F,A为C上的点,以F为圆心,
(p>0)的焦点为F,A为C上的点,以F为圆心,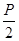 为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠
为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠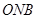 = .
= .
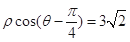 ,曲线
,曲线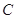 :
: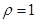 上的点到直线的距离为
上的点到直线的距离为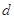 ,则
,则