题目内容
已知函数 ,其中
,其中
(1)若曲线
 在点
在点 处的切线方程为y=3x+1,求函数
处的切线方程为y=3x+1,求函数 的解析式;
的解析式;
(2)讨论函数 的单调性;[来
的单调性;[来
解:(1)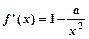 ,由导数的几何
,由导数的几何 意义得
意义得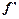
(2)=3,于是a=-8,
由切点P(2,f(2))在直线y=3x+1上可得-2+b=7,解得b=9
所以函数f(x)的解析式为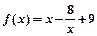
(2)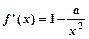 ,当a≤0时,
,当a≤0时,
显然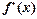 >0(x≠0),这时f(x)在(-∞,0),(0,+∞)内是增函数;
>0(x≠0),这时f(x)在(-∞,0),(0,+∞)内是增函数;
当a>0时,令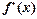 =0,解得x=
=0,解得x=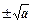 ,[来源:Z.xx.k.Com]
,[来源:Z.xx.k.Com]
当x变化时,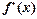 ,
, 的变化情况如下表:[来源:学_科_网]
的变化情况如下表:[来源:学_科_网]x (-∞,- 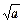 )
)- 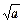
(- 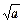 ,
, 0)
0)(0, 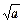 )
)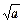
( 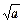 ,+∞)
,+∞)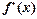
+ 0 - - 0 + 

极大值 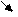

极小值 
所以 在(-∞,-
在(-∞,-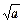 ),(
),(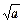 ,+∞)内是增函数,在(-
,+∞)内是增函数,在(-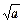 ,0),(0,
,0),(0, 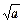
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f'(0)=2,则
 =( )
=( )
| A.4 | B.-8 | C.0 | D.8 |
sin570°的值是 ( )
A. | B.- | C. | D.- |
 =" " ( )
=" " ( )
| A.—6 | B.0 | C.6 | D.3 |
 上的函数
上的函数 ,其中
,其中 为常数.
为常数. 是函数
是函数 的一个极值点,求
的一个极值点,求 间
间 上是增函数,求
上是增函数,求 ,在
,在 处取得最大值,求正数
处取得最大值,求正数 ,Q=
,Q= t.今该公司将5
t.今该公司将5 为自然对数的底数
为自然对数的底数
 时,求函数
时,求函数 的极值;
的极值; 的取值范围.
的取值范围. 数
数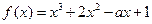 .
. 在点
在点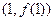 处的切线斜率为4,求实
处的切线斜率为4,求实 数
数 的值;
的值;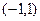 上是单调函数,求实数
上是单调函数,求实数 = .
= .