题目内容
11.数列{an}为等差数列,a10=33,a2=1,Sn为数列{an}的前n项和,则S20-2S10等于( )| A. | 40 | B. | 200 | C. | 400 | D. | 20 |
分析 根据前n项和公式求出首项和公差即可得到结论.
解答 解:∵a10=33,a2=1,
∴a10=a2+8d,
即d=$\frac{{a}_{10}-{a}_{2}}{8}=\frac{33-1}{8}=\frac{32}{8}=4$,
则首项a1=1-4=-3,
则S20-2S10=20×(-3)+$\frac{20×19}{2}×4$-2[10×(-3)+$\frac{10×9}{2}×4$]
=-60+760-2(-30+180)
=700-300=400.
故选:C
点评 本题主要考查等差数列前n项和公式的应用,根据条件求出首项和公差是解决本题的关键.

练习册系列答案
相关题目
2.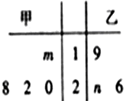 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )| A. | $\frac{1}{8}$ | B. | 8 | C. | 9 | D. | $\frac{1}{9}$ |
6.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了四次试验如下:
(1)求y关于x的线性回归方程
(2)试预测加工10个零件需要多少时间?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$ $\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 零件的个数x/个 | 2 | 3 | 4 | 5 |
| 加工的时间y/小时 | 2.5 | 3 | 4 | 4.5 |
(2)试预测加工10个零件需要多少时间?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$ $\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
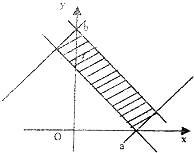 设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.
设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.