题目内容
6.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了四次试验如下:| 零件的个数x/个 | 2 | 3 | 4 | 5 |
| 加工的时间y/小时 | 2.5 | 3 | 4 | 4.5 |
(2)试预测加工10个零件需要多少时间?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$ $\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
分析 (1)根据表中所给的数据,做出横标和纵标的平均数,得到样本中心点,求出对应的横标和纵标的积的和,求出横标的平方和,根据最小二乘法做出系数b和代入样本中心点求出a的值,写出线性回归方程.
(2)将x=10代入回归直线方程,得y=0.7×10+1.05=8.05,可以预测加工10个零件需要8.05个小时,这是一个预报值,不是生产10个零件的准确的时间数.
解答 解:(1)$\overline{x}$=3.5,$\overline{y}$=3.5,
xiyi=2×2.5+3×3+4×4+5×4.5=52.5,xi2=4+9+16+25=54,
∴b=0.7,a=3.5-0.7×3.5=1.05,
∴回归直线方程为y=0.7x+1.05.
(2)当x=10时,=0.7×10+1.05=8.05,
∴预测加工10个零件需要8.05小时.
点评 本题考查线性回归方程的求法和应用,解题的关键是正确应用最小二乘法求出线性回归方程的系数的运算,再一点就是代入样本中心点可以求出字母a的值,本题运算比较繁琐,本题是一个中档题目.

练习册系列答案
相关题目
2.定义在R上的偶函数f(x)满足f(x+2)=f(x),且在区间[-3,-2]上是减函数,若A,B是锐角三角形的两个内角,且A>B,则( )
| A. | f(sinA)>f(cosB) | B. | f(sinA)<f(cosB) | C. | f(sinA)>f(sinB) | D. | f(cosA)>f(cosB) |
3.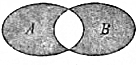 如图所示的韦恩图中,A,B中两非空集合,定义集合A?B为阴影部分表示的集合,若x,y∈R,A={x|y=ln(2x-x2)},B={y|y=ex,x>0},则A?B为( )
如图所示的韦恩图中,A,B中两非空集合,定义集合A?B为阴影部分表示的集合,若x,y∈R,A={x|y=ln(2x-x2)},B={y|y=ex,x>0},则A?B为( )
 如图所示的韦恩图中,A,B中两非空集合,定义集合A?B为阴影部分表示的集合,若x,y∈R,A={x|y=ln(2x-x2)},B={y|y=ex,x>0},则A?B为( )
如图所示的韦恩图中,A,B中两非空集合,定义集合A?B为阴影部分表示的集合,若x,y∈R,A={x|y=ln(2x-x2)},B={y|y=ex,x>0},则A?B为( )| A. | {x|0<x<2} | B. | {x|x≤1或x≥2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0<x≤1或x≥2} |
11.数列{an}为等差数列,a10=33,a2=1,Sn为数列{an}的前n项和,则S20-2S10等于( )
| A. | 40 | B. | 200 | C. | 400 | D. | 20 |
18.已知集合A={x|0<x<1|,B={x|-1≤log2x≤1},则A∩B=( )
| A. | (0,2] | B. | [$\frac{1}{2}$,1) | C. | (1,2] | D. | [$\frac{1}{2}$,2] |
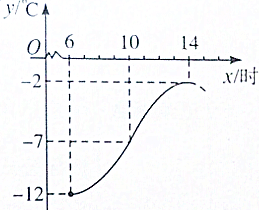 如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).
如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).