题目内容
（文科）已知△ABC中，A：B：C=1：2：3，a=1，则
= ．
| a |
| sinA |
考点：正弦定理
专题：解三角形
分析：由三角之比，利用内角和定理求出A的度数，将a与sinA的值代入计算即可求出值．
解答：
解：∵△ABC中，A：B：C=1：2：3，
∴A=30°，B=60°，C=90°，
∵a=1，
∴
=
=2．
故答案为：2
∴A=30°，B=60°，C=90°，
∵a=1，
∴
| a |
| sinA |
| 1 | ||
|
故答案为：2
点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
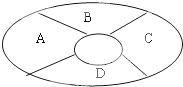如图，A，B，C，D四个区域，现在有4种不同的颜色，给A，B，C，D四个区域涂色，要求每个区域只涂一色且相邻区域不涂同一色，则不同的涂法有
如图，PC切圆O于点C，割线PAB经过圆心0，弦CD⊥AB于点E．已知圆O的半径为3，PA=2，则PC=（文科）在数列{an}中，a1=-2，an+1=1-
，则a2013的值为（ ）
| 1 |
| an |
| A、-2 | ||
B、
| ||
C、
| ||
D、
|