题目内容
四面体A-BCD中，AB=CD=1，其余各棱长均为2，则VA-BCD=_________．
分析：根据三棱锥A-BCD中，AB=CD=1，其余各棱长均为2，将三棱锥A-BCD中放置在一个长方体中，如图，设长方体的长，宽，高分别为：a，b，c．利用直角三角形的边的关系建立
，由此结合它们体积间的关系，推算出四面体A-BCD的体积．解答：
解：将三棱锥A-BCD中放置在一个长方体中，如图：设长方体的长，宽，高分别为：a，b，c．
则有：
∴a2=
，b2=c2=
．长方体的体积为：V=
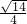
又四面体A-BCD的体积是长方体体积的
．故答案为：
．点评：本题考查棱柱、棱锥、棱台的体积，构造长方体是解题的难点．
练习册系列答案
相关题目
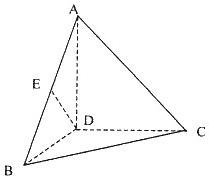如图，四面体A-BCD中，AD⊥BD，AD⊥CD，BD⊥CD，且AD=BD=CD=2，点E是线段AB的中点．
设正四面体A-BCD中，E、F分别为AC、AD的中点，则△BEF在该四面体的面ADC上的射影可能是（ ）