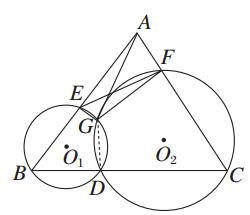
题目内容
(本小题满分12分) 已知圆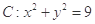 ,点
,点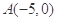 ,直线
,直线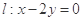 .
.
(1) 求与圆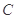 相切,且与直线
相切,且与直线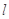 垂直的直线方程;
垂直的直线方程;
(2) 在直线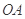 上(
上(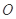 为坐标原点),存在定点
为坐标原点),存在定点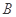 (不同于点
(不同于点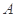 ),满足:对于圆
),满足:对于圆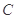 上任一点
上任一点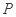 ,都有
,都有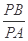 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点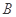 的坐标.
的坐标.
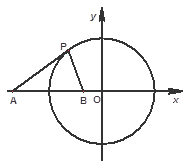
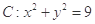 ,点
,点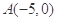 ,直线
,直线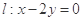 .
.(1) 求与圆
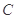 相切,且与直线
相切,且与直线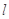 垂直的直线方程;
垂直的直线方程;(2) 在直线
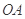 上(
上(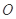 为坐标原点),存在定点
为坐标原点),存在定点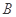 (不同于点
(不同于点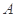 ),满足:对于圆
),满足:对于圆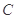 上任一点
上任一点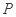 ,都有
,都有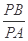 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点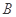 的坐标.
的坐标.
(1) ;(2)存在,且
;(2)存在,且 .
.
 ;(2)存在,且
;(2)存在,且 .
.试题分析:(1)充分利用垂直直线系方程设直线方程,即若直线
 垂直于直线
垂直于直线 ,则可设直线
,则可设直线 方程为:
方程为: ,并利用圆与直线相切时,圆心到直线的距离等于半径的几何性质性质求解得直线方程;(2)假设存在,利用条件表达出
,并利用圆与直线相切时,圆心到直线的距离等于半径的几何性质性质求解得直线方程;(2)假设存在,利用条件表达出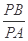 并利用坐标化简求解.
并利用坐标化简求解.试题解析:
⑴因所求直线垂直于直线
 ,故设所求直线方程为
,故设所求直线方程为 ,
, 直线与圆相切,∴
直线与圆相切,∴ ,得
,得 ,∴所求直线方程为
,∴所求直线方程为 .
.⑵假设存在这样的点
 ,当
,当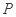 为圆
为圆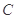 与
与 轴左交点
轴左交点 时,
时, ;
;当
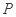 为圆
为圆 与
与 轴右交点
轴右交点 时,
时, ,依题意,
,依题意, ,
,解得,
 (舍去),或
(舍去),或 .
.下面证明 点
 对于圆
对于圆 上任一点
上任一点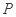 ,都有
,都有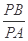 为一常数.
为一常数.设
 ,则
,则 ,
,∴
 ,
,从而
 为常数.
为常数.
练习册系列答案
相关题目
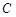 :
: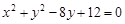 ,直线
,直线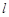 经过点
经过点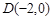 ,
, 为直径的圆
为直径的圆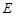 的方程;
的方程;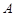 ,
,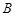 两点,且
两点,且 为等腰直角三角形,求直线
为等腰直角三角形,求直线
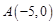 ,
,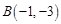 ,若圆
,若圆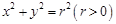 上恰有两点
上恰有两点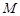 ,
,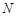 ,使得
,使得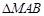 和
和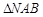 的面积均为
的面积均为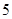 ,则
,则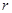 的取值范围是 .
的取值范围是 . 与曲线
与曲线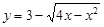 有公共点,则
有公共点,则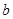 的取值范围是 .
的取值范围是 .