题目内容
(1)求直线l1:2x+3y=12和l2:x-2y=4交点的坐标;
(2)求点A(-2,3)到直线l:3x+4y+3=0的距离.
(2)求点A(-2,3)到直线l:3x+4y+3=0的距离.
(1)∵直线l1:2x+3y=12和l2:x-2y=4,
∴联解
,可得
,
因此,直线l1和l2交点的坐标为(
,
);
(2)∵点A(-2,3),直线l方程为3x+4y+3=0,
∴由点到直线的距离公式,
得点A到直线l的距离为d=
=
.
∴联解
|
|
因此,直线l1和l2交点的坐标为(
| 6 |
| 7 |
| 36 |
| 7 |
(2)∵点A(-2,3),直线l方程为3x+4y+3=0,
∴由点到直线的距离公式,
得点A到直线l的距离为d=
| |3×(-2)+4×3+3| | ||
|
| 9 |
| 5 |

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
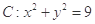 ,点
,点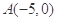 ,直线
,直线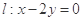 .
.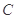 相切,且与直线
相切,且与直线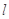 垂直的直线方程;
垂直的直线方程;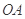 上(
上(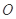 为坐标原点),存在定点
为坐标原点),存在定点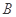 (不同于点
(不同于点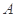 ),满足:对于圆
),满足:对于圆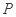 ,都有
,都有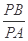 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点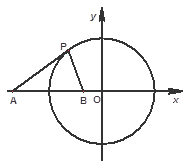
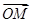 ·
·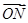 (O为坐标原点)等于( )
(O为坐标原点)等于( )