Question

（本题满分13分）

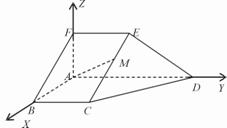
如图，在五面体ABCDEF中，FA平面ABCD，AD//BC//FE，ABAD，AF＝AB＝BC＝FE＝AD

（Ⅰ）求异面直线BF与DE所成角的余弦值；

（Ⅱ）在线段CE上是否存在点M，使得直线AM与平面CDE所成角的正弦值为？若存在，试确定点M的位置；若不存在，请说明理由.

Answer 1

（13分）

解法一：建立如图所示的直角坐标系，不妨设AB＝１

则                             ………………2分

（Ⅰ）

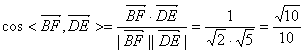　　　　　                 ………………5分

　　　　异面直线BF与DE所成角的余弦值为.                    ………………6分

　　（Ⅱ）设平面CDE的一个法向量为

　　

　　得

   

令                                         ………………9分

　设存在点M满足条件，由

　　　直线AM与平面CDE所成角的正弦值为

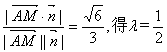　　                   ………………12分

　　故当点M为CE中点时，直线AM与面CDE所成角的正弦值为.         ………13分

解法二：（Ⅰ）不妨设AB＝１，且

∴∠CED异面直线BF与DE所成角                                                         ………………3分

CE=BF=,ED=DC=,

所以，异面直线BF与DE所成角的余弦值为                                     ………………6分

　　（Ⅱ）与解法一同.