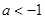题目内容
已知函数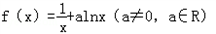
(Ⅰ)若a=1,求函数f(x)的极值和单调区间;
(II)若在区间[1,e]上至少存在一点x0,使得f(x0)<0成立,求实数a的取值范围.
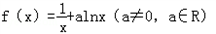
(Ⅰ)若a=1,求函数f(x)的极值和单调区间;
(II)若在区间[1,e]上至少存在一点x0,使得f(x0)<0成立,求实数a的取值范围.
解:(I)因为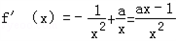 ,
,
当a=1,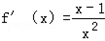 ,令f '(x)=0,得x=1,
,令f '(x)=0,得x=1,
又f(x)的定义域为(0,+∞),f '(x),f(x)随x的变化情况如下表:

所以x=1时,f(x)的极小值为1.
f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1);
(II)因为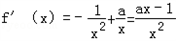 ,且a≠0,
,且a≠0,
令f '(x)=0,得到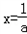 ,若在区间[1,e]上存在一点x0,使得f(x0)<0成立,
,若在区间[1,e]上存在一点x0,使得f(x0)<0成立,
其充要条件是f(x)在区间[1,e]上的最小值小于0即可.
(1)当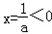 ,即a<0时,f '(x)<0对x∈(0,+∞)成立,
,即a<0时,f '(x)<0对x∈(0,+∞)成立,
所以,f(x)在区间[1,e]上单调递减,
故f(x)在区间[1,e]上的最小值为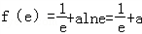 ,
,
由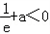 ,得
,得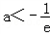 ,即
,即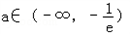
(2)当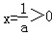 ,即a>0时,
,即a>0时,
①若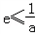 ,则f '(x)≤ 0对x∈[1,e]成立,所以f(x)在区间[1,e]上单调递减,
,则f '(x)≤ 0对x∈[1,e]成立,所以f(x)在区间[1,e]上单调递减,
所以,f(x)在区间[1,e]上的最小值为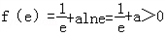 ,
,
显然,f(x)在区间[1,e]上的最小值小于0不成立
②若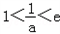 ,即
,即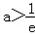 时,则有
时,则有

所以f(x)在区间[1,e]上的最小值为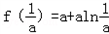 ,由
,由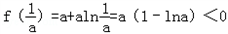 ,得1﹣lna<0,解得a>e,
,得1﹣lna<0,解得a>e,
即a∈(e,+∞).
由(1)(2)可知: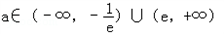 符合题意.
符合题意.
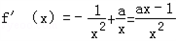 ,
,当a=1,
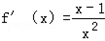 ,令f '(x)=0,得x=1,
,令f '(x)=0,得x=1,又f(x)的定义域为(0,+∞),f '(x),f(x)随x的变化情况如下表:

所以x=1时,f(x)的极小值为1.
f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1);
(II)因为
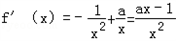 ,且a≠0,
,且a≠0,令f '(x)=0,得到
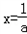 ,若在区间[1,e]上存在一点x0,使得f(x0)<0成立,
,若在区间[1,e]上存在一点x0,使得f(x0)<0成立,其充要条件是f(x)在区间[1,e]上的最小值小于0即可.
(1)当
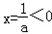 ,即a<0时,f '(x)<0对x∈(0,+∞)成立,
,即a<0时,f '(x)<0对x∈(0,+∞)成立,所以,f(x)在区间[1,e]上单调递减,
故f(x)在区间[1,e]上的最小值为
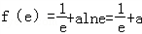 ,
,由
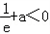 ,得
,得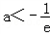 ,即
,即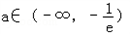
(2)当
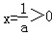 ,即a>0时,
,即a>0时,①若
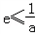 ,则f '(x)≤ 0对x∈[1,e]成立,所以f(x)在区间[1,e]上单调递减,
,则f '(x)≤ 0对x∈[1,e]成立,所以f(x)在区间[1,e]上单调递减,所以,f(x)在区间[1,e]上的最小值为
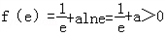 ,
,显然,f(x)在区间[1,e]上的最小值小于0不成立
②若
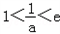 ,即
,即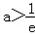 时,则有
时,则有
所以f(x)在区间[1,e]上的最小值为
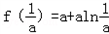 ,由
,由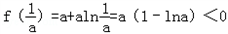 ,得1﹣lna<0,解得a>e,
,得1﹣lna<0,解得a>e,即a∈(e,+∞).
由(1)(2)可知:
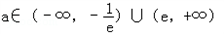 符合题意.
符合题意.
练习册系列答案
相关题目

 ,求f(x)的解析式.
,求f(x)的解析式.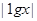 ,若a < b,且f(a) = f(b),则a + 2b的取值范围是________ .
,若a < b,且f(a) = f(b),则a + 2b的取值范围是________ .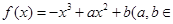 R).
R).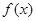 的图象能否总在直线
的图象能否总在直线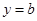 的下方?说明理由;
的下方?说明理由;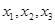 为方程
为方程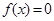 的三个根,且
的三个根,且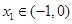 ,
,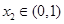 ,
,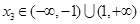 , 求证:
, 求证: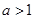 或
或