题目内容
(本小题满分12分)
已知函数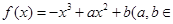 R).
R).
(Ⅰ)若a=1,函数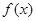 的图象能否总在直线
的图象能否总在直线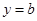 的下方?说明理由;
的下方?说明理由;
(Ⅱ)若函数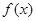 在(0,2)上是增函数,求a的取值范围;
在(0,2)上是增函数,求a的取值范围;
(Ⅲ)设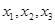 为方程
为方程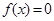 的三个根,且
的三个根,且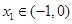 ,
,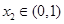 ,
,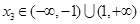 , 求证:
, 求证: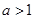 或
或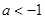
【答案】
(Ⅰ),函数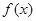 的图象不能总在直线
的图象不能总在直线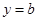 的下方.
的下方.
(Ⅱ)a的取值范围为
(Ⅲ)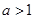 或
或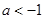
【解析】(Ⅰ)解:当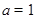 时,
时,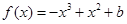 ,
,
因为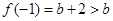 ,
,
所以,函数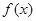 的图象不能总在直线
的图象不能总在直线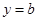 的下方.
的下方.
(Ⅱ)解:由题意,得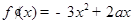 ,
,
令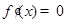 ,解得
,解得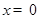 或
或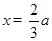 ,
-
,
-
①当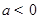 时,由
时,由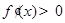 ,解得
,解得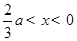 ,
,
所以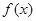 在
在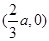 上是增函数,与题意不符,舍去;
上是增函数,与题意不符,舍去;
②当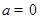 时,由
时,由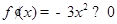 ,与题意不符,舍去;
,与题意不符,舍去;
③当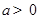 时,由
时,由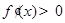 ,解得
,解得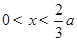 ,
,
所以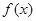 在
在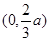 上是增函数,
上是增函数,
又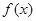 在(0,2)上是增函数,所以
在(0,2)上是增函数,所以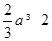 ,解得
,解得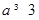 ,
,
综上,a的取值范围为 .
.
(Ⅲ)解:因为方程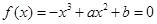 最多只有3个根,
最多只有3个根,
由题意,得在区间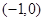 内仅有一根,
内仅有一根,
所以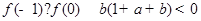 ,
,
同理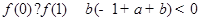 ,
,
①当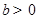 时,由1得
时,由1得 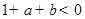 ,即
,即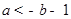 ,
,
由2得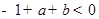 ,即
,即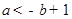 ,
,
因为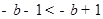 ,所以
,所以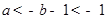 ,即
,即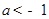 ;
;
②当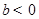 时,由1得
时,由1得 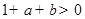 ,即
,即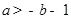 ,
,
由2得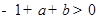 ,即
,即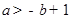 ,
,
因为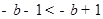 ,所以
,所以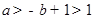 ,即
,即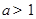 ;
;
③当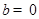 时,因为
时,因为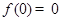 ,所以
,所以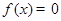 有一根0,
有一根0,
这与题意不符. ∴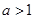 或
或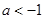 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目