题目内容
已知a∈R,函数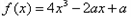 。
。
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+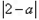 >0。
>0。
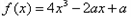 。
。(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+
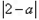 >0。
>0。解:(1)由题意得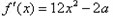 ,当
,当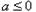 时,
时,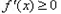 恒成立,
恒成立,
此时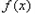 的单调递增区间为
的单调递增区间为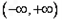
当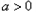 时,
时,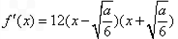 ,
,
此时函数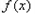 的单调递增区间为
的单调递增区间为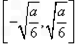 .
.
(2)由于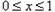 ,当
,当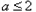 时,
时,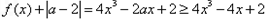
当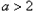 时,
时,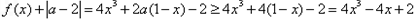
设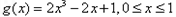 ,则
,则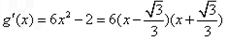
则有: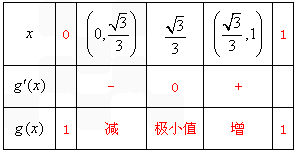
所以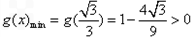
当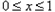 时,
时,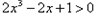
故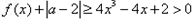 。
。

练习册系列答案
相关题目
题目内容
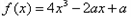 。
。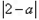 >0。
>0。解:(1)由题意得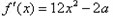 ,当
,当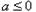 时,
时,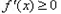 恒成立,
恒成立,
此时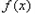 的单调递增区间为
的单调递增区间为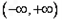
当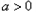 时,
时,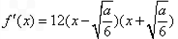 ,
,
此时函数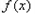 的单调递增区间为
的单调递增区间为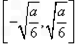 .
.
(2)由于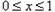 ,当
,当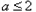 时,
时,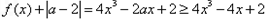
当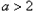 时,
时,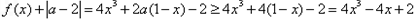
设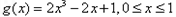 ,则
,则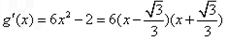
则有:
所以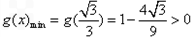
当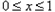 时,
时,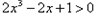
故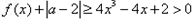 。
。
