题目内容
12.已知数列{an}满足a1=1,且对任意n≥2,n∈N*都有an=2an-1+1,则a5=31.分析 化简可得an+1=2(an-1+1),从而数列{an+1}是以2为首项,2为公比的等比数列,求出an的通项公式,即可求出答案.
解答 解:∵an=2an-1+1,
∴an+1=2(an-1+1),
∴$\frac{{a}_{n}+1}{{a}_{n-1}+1}$=2,
∵a1=1,
∴a1+1=2,
∴数列{an+1}是以2为首项,2为公比的等比数列,
∴an+1=2n,
∴an=2n-1,
∴a5=25-1=31
故答案为:31.
点评 本题考查了构造法的应用及等比数列的判断与应用,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.当下社会热议中国人口政策,下表是中国人民大学人口预测课题组根据我过2000年第五次人口普查预测的15-64岁劳动人口所占比例:
根据上表,y关于t的线性回归方程为y=-1.7t+68.7
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{y})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-t)^{2}}$,$\overline{a}$=$\overline{y}$-$\overline{b}$$\overline{t}$.
| 年份 | 2030 | 2035 | 2040 | 2045 | 2050 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 所占比例y | 68 | 65 | 62 | 62 | 61 |
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{y})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-t)^{2}}$,$\overline{a}$=$\overline{y}$-$\overline{b}$$\overline{t}$.
7.已知a,b∈R,则使不等式|a+b|<|a|+|b|一定成立的条件是( )
| A. | a+b>0 | B. | a+b<0 | C. | ab>0 | D. | ab<0 |
17.某几何体的三视图及其尺寸如图所示,则该几何体的各侧面中,最大的侧面的面积为( )
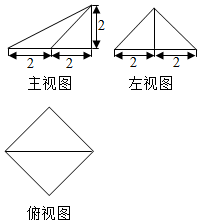

| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
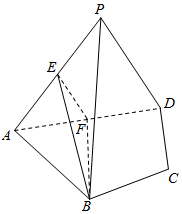 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.求证:
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.求证: