题目内容
15．向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为θ，则称$\overrightarrow{a}$◎$\overrightarrow{b}$为$\overrightarrow{a}$，$\overrightarrow{b}$的积，定义$\overrightarrow{a}$◎$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|tanθ，若|$\overrightarrow{a}$|=5，|$\overrightarrow{b}$|=1，$\overrightarrow{a}$•$\overrightarrow{b}$=-3，则$\overrightarrow{a}$◎$\overrightarrow{b}$等于（ ）| A． | $-\frac{20}{3}$ | B． | $\frac{20}{3}$ | C． | 4 | D． | -4 |
分析 通过向量的数量积求出cosθ，然后求出sinθ，tanθ，利用新定义求解即可．
解答 解：由已知得$\overrightarrow{a}$•$\overrightarrow{b}$=-3=|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=5cosθ，
所以cosθ=-$\frac{3}{5}$，
所以sinθ=$\frac{4}{5}$，tanθ=$\frac{sinθ}{cosθ}$=-$\frac{4}{3}$，
根据定义，知$\overrightarrow{a}$◎$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|tanθ=5×$（-\frac{4}{3}）$=-$\frac{20}{3}$．
故选：A．
点评 本题考查向量的数量积的应用，新定义的应用，基本知识的考查．
练习册系列答案
相关题目
5．若函数f（x）=2sin（ωx-$\frac{π}{3}$）（ω≠0），且f（2+x）=f（2-x），则|ω|的最小值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{5π}{12}$ | D． | $\frac{5π}{6}$ |
6．已知某几何体的三视图的侧视图是一个正三角形，如图所示，则该几何体的表面积等于（ ）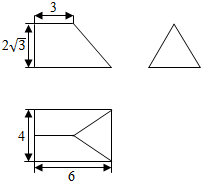
| A． | 60+4$\sqrt{3}$+2$\sqrt{21}$ | B． | 60+2$\sqrt{3}$+2$\sqrt{21}$ | C． | 60+2$\sqrt{3}$+4$\sqrt{21}$ | D． | 60+4$\sqrt{3}$+4$\sqrt{21}$ |
10．已知中心在原点的椭圆C以抛物线y2=4x的焦点F为右焦点，且它们的公共点P到点F的距离为$\frac{5}{3}$，则椭圆C的标准方程为（ ）
| A． | $\frac{{x}^{2}}{4}$+y2=1 | B． | $\frac{{y}^{2}}{4}$+x2=1 | C． | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D． | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |
7．若偶函数f（x）在[0，2]上单调递减，则（ ）
| A． | f（-1）＞f $（{{{log}_{0.5}}\frac{1}{4}}）$＞f（lg0.5） | B． | f（lg0.5）＞f（-1）＞f $（{{{log}_{0.5}}\frac{1}{4}}）$ | ||
| C． | f $（{{{log}_{0.5}}\frac{1}{4}}）$＞f（-1）＞f（lg0.5） | D． | f（lg0.5）＞f $（{{{log}_{0.5}}\frac{1}{4}}）$＞f（-1） |
4．
如图，在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器，圆锥的上底圆周与鱼缸的底面正方形相切，圆锥的顶点在鱼缸的缸底上，现在向鱼缸内随机地投入一粒鱼食，则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是（ ）
如图，在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器，圆锥的上底圆周与鱼缸的底面正方形相切，圆锥的顶点在鱼缸的缸底上，现在向鱼缸内随机地投入一粒鱼食，则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是（ ）| A． | 1-$\frac{π}{4}$ | B． | $\frac{π}{12}$ | C． | $\frac{π}{4}$ | D． | 1-$\frac{π}{12}$ |