题目内容
1.已知函数f(x)在定义域(0,+∞)上是单调函数,若对任意的x∈(0,+∞),都有f[f($\frac{1}{x}$)-x]=2,则f′($\frac{1}{2}$)=-4.分析 首先,根据函数f(x)在定义域(0,+∞)上是单调函数,若对任意x∈(0,+∞),都有f[f($\frac{1}{x}$)-x]=2,得到f($\frac{1}{x}$)-x为一个常数,以t换$\frac{1}{x}$,得f(t)-$\frac{1}{t}$=n,则f(t)-$\frac{1}{t}$=n,f(n)=2,求出n,即可求出函数的解析式,求导,即可得出结论.
解答 解:根据题意,得若对任意x∈(0,+∞),都有f[f($\frac{1}{x}$)-x]=2,得到f($\frac{1}{x}$)-x为一个常数,
以t换$\frac{1}{x}$,得f(t)-$\frac{1}{t}$=n,
则f(t)-$\frac{1}{t}$=n,f(n)=2,
∴f(t)=$\frac{1}{t}$+n,
∴f(n)=$\frac{1}{n}$+n=2,
∴n=1,
∴f(x)=1+$\frac{1}{x}$,
∴f′(x)=-$\frac{1}{{x}^{2}}$,
∴f′($\frac{1}{2}$)=-4.
故答案为:-4.
点评 本题考查的知识点是函数的值,函数解析式的求法,其中抽象函数解析式的求法,要注意对已知条件及未知条件的凑配思想的应用.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
12.数列{an}的通项an=sin$\frac{nπ}{3}$,前n项和为Sn,则S2015等于( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | -$\frac{1}{2}$ |
9.已知x>y>0,a=log2(x3+y3),b=log2(x2y+xy2),c=1+$\frac{3}{2}$log2xy,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
10.已知函数f(x)=-x2+2ax+1-a在区间[0,1]上的最大值为2,则a的值为( )
| A. | 2 | B. | -1或-3 | C. | 2或-3 | D. | -1或2 |
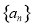 的前
的前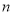 项和为
项和为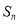 ,
,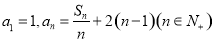 .
.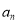 和
和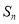 ;
; 的前
的前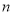 项和为
项和为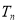 ,证明:
,证明: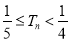 .
.