题目内容
11.已知f(x)是二次函数,若f(0)=3,且其图象的顶点坐标为(2,-3).(1)求f(x)解析式;
(2)求函数y=f(x2-1)的值域.
分析 (1)设出函数的顶点式,将(0,3)代入可得f(x)解析式;
(2)令t=x2-1,则t≥-1,结合二次函数的图象和性质,可得函数y=f(x2-1)的值域.
解答 解:(1)∵二次函数f(x)图象的顶点坐标为(2,-3).
∴设f(x)=a(x-2)2-3,
又∵f(0)=3,
∴4a-3=3,
∴a=$\frac{3}{2}$,
∴f(x)=$\frac{3}{2}$(x-2)2-3=$\frac{3}{2}$x2-6x-3:
(2)令t=x2-1,则t≥-1,
又∵函数f(x)的图象开口朝上,且以直线x=2为对称轴,
故t=2时,函数取最小值-3,无最大值;
即函数y=f(x2-1)的值域为[-3,+∞)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.直线(m+2)x+(1-m)y-6=0与圆(x-2)2+y2=1的位置关系是( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 以上都有可能 |
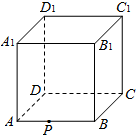 如图所示,在正方体ABCD-A1B1C1D1中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和平面ABC1D1均成30°角,则这样的直线l有( )
如图所示,在正方体ABCD-A1B1C1D1中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和平面ABC1D1均成30°角,则这样的直线l有( )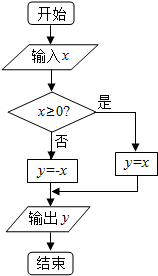 阅读如图所示的程序框图.
阅读如图所示的程序框图.