题目内容
18.不等式ax2-2ax-4<0对一切实数都成立.求实数a的取值范围.分析 讨论a=0与a≠0时,不等式ax2-2ax-4<0对一切实数x恒成立的情况,求出a的取值范围即可.
解答 解:a=0时,-4<0,对一切实数x都成立,满足题意;
a≠0时,一元二次不等式ax2-2ax-4<0对一切x∈R恒成立,
则$\left\{\begin{array}{l}{a<0}\\{{(-2a)}^{2}-4a×(-4)<0}\end{array}\right.$,
解得-4<a<0;
综上,a的取值范围是{a|-4<a≤0}.
点评 本题考查了含参数的不等式的解法与应用问题,解题时注意利用数形结合思想以及判别式的应用,是基础题目.

练习册系列答案
相关题目
13.若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ x-5y+10≤0\\ x+y-8≤0\end{array}\right.$所表示的平面区域存在点(x0,y0)使ax0+y0+2≤0成立,则实数a的取值范围是( )
| A. | a≤1 | B. | a≤-1 | C. | a≥1 | D. | a≥-1 |
3.已知点A(2,-1,5),B(t,t+1,t-1),则|AB|取得最小值时,t的值等于( )
| A. | $\sqrt{15}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{30}$ | D. | 2 |
10.在屠哟哟获得2015年诺贝尔生理学或医学奖后,某市在两所学铰之间举办了学习交流会,两所学饺各选派3名学生代表,校际间轮流发言,那么不同的发言顺序共有( )
| A. | 72种 | B. | 36种 | C. | 144种 | D. | 108种 |
7.在等比数列{an}中,已知a1=1,q=2,则第5项至第10项的和为( )
| A. | 63 | B. | 992 | C. | 1008 | D. | 1023 |
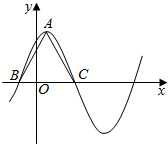 函数$f(x)=6{cos^2}\frac{ωx}{2}+\sqrt{3}sinωx-3({ω>0})$在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
函数$f(x)=6{cos^2}\frac{ωx}{2}+\sqrt{3}sinωx-3({ω>0})$在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.