题目内容
13.已知函数f(x)=$\frac{ax-a}{{e}^{x}}+1$有且仅有两个零点,则实数a的取值范围为( )| A. | (-e2,0] | B. | (-∞,-e2) | C. | [-e2,0] | D. | [-e2,+∞) |
分析 令f(x)=0,可得a(x-1)=-ex,可得a=$\frac{{e}^{x}}{1-x}$在x≠1有且只有2个不等实根,等价为函数g(x)=$\frac{{e}^{x}}{1-x}$的图象和直线y=a有且只有两个交点.求出g(x)的导数和单调区间、极值,即可得到所求a的范围.
解答 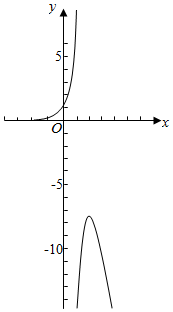 解:f(x)=$\frac{ax-a}{{e}^{x}}+1$,
解:f(x)=$\frac{ax-a}{{e}^{x}}+1$,
令f(x)=0,可得a(x-1)=-ex,
当x=1时,上式显然不成立;
可得a=$\frac{{e}^{x}}{1-x}$在x≠1有且只有2个不等实根,
等价为函数g(x)=$\frac{{e}^{x}}{1-x}$的图象和直线y=a有且只有两个交点.
由g′(x)=$\frac{{e}^{x}(2-x)}{(1-x)^{2}}$,可得x>2时,g′(x)<0,g(x)递减;
当x<1或1<x<2时,g′(x)>0,g(x)递增.
即有x=2处,g(x)取得极大值-e2.
作出函数g(x)的图象,如右:
由图象可得a<-e2时,直线y=a和y=g(x)的图象有两个交点.
故选:B.
点评 本题考查函数的零点个数问题解法,注意运用函数方程的转化思想和数形结合思想方法,考查导数的运用:求单调区间和极值,考查运算能力,属于中档题.

练习册系列答案
相关题目
4.已知三棱柱ABC-A1B1C1的底面ABC是边长为1的正三角形,侧棱AA1与底面所成的角是60°,在侧棱AA1,BB1,CC1上分别有点P,Q,R且AP=$\frac{3}{2}$,BQ=1,CR=$\frac{1}{2}$,则截面PQR与底面ABC之间的几何体的体积是( )
| A. | $\frac{3}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.某单位从6男4女共10名员工中,选出3男2女共5名员工,安排在周一到周五的5个夜晚值班,每名员工值一个夜班且不重复值班,其中女员工甲不能安排在星期一、星期二值班,男员工乙不能安排在星期二值班,其中男员工丙必须被选且必须安排在星期五值班,则这个单位安排夜晚值班的方案共有( )
| A. | 960种 | B. | 984种 | C. | 1080种 | D. | 1440种 |
2.已知等差列{an}的前n项和为Sn,且a2+a4=16,则S5=( )
| A. | -31 | B. | 20 | C. | 31 | D. | 40 |
9.某学校高三年级有2个文科班,3个理科班,现每个班制定1人对各班的卫生进行检查,若每班只安排一人检查,且文科班学生不检查文科班,理科班学生不检查自己所在的班,则不同安排方法的种数是( )
| A. | 24 | B. | 48 | C. | 72 | D. | 144 |
18.若随机变量X的分布列为
则D(X)=$\frac{2}{9}$.
| X | 0 | 1 |
| P | $\frac{2}{3}$ | m |
4.已知y=f(x)为定义在R上的单调递增函数,y=f′(x)是其导函数,若对任意∈R总有$\frac{f(x)}{f′(x)}$<$\frac{1}{2017}$,则下列大小关系一定正确的是( )
| A. | f($\frac{1}{2017}$)>e•f(0) | B. | f($\frac{1}{2017}$)<e•f(0) | C. | f($\frac{1}{2017}$)>e2•f(0) | D. | f($\frac{1}{2017}$)<e2•f(0) |
 的值为( )
的值为( )
 B.
B.
 D.
D.