题目内容
已知函数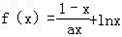
．
（1）当a=1时，求f（x）的最小值；
（2）若函数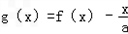
在区间（1，2）上不单调，求a的取值范围．
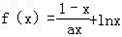．（1）当a=1时，求f（x）的最小值；
（2）若函数
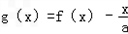在区间（1，2）上不单调，求a的取值范围．解：（1）当
，
令f'（x）=0得x=1．
f'（x）＜0得0＜x＜1，
f'（x）＞0得1＜x，
∴f（x）在（0，1）上单调递减，在（1，+∞）上单调递增．
故fmin（x）=f（1）=0．
（2）
.
．
∵g（x）在（1，2）上不单调，
∴x2﹣ax+1=0在（1，2）上有根且无重根．
即方程
在（1，2）有根，且无重根．
∴
．
，令f'（x）=0得x=1．
f'（x）＜0得0＜x＜1，
f'（x）＞0得1＜x，
∴f（x）在（0，1）上单调递减，在（1，+∞）上单调递增．
故fmin（x）=f（1）=0．
（2）
.．∵g（x）在（1，2）上不单调，
∴x2﹣ax+1=0在（1，2）上有根且无重根．
即方程
在（1，2）有根，且无重根．∴
．
练习册系列答案
相关题目
．
只有一个零点；
函数
．
．
的极小值；
，x∈[-1，1]，求
的最大值F（a）．
．
时，f（x）的值域为[4，6]，求a，b的值．
函数
．