题目内容
已知函数![]() ,当点
,当点![]() 在
在![]() 的图像上移动时,
的图像上移动时,
点![]() 在函数
在函数![]() 的图像上移动.
的图像上移动.
(1) 若点P坐标为(![]() ),点Q也在
),点Q也在![]() 的图像上,求
的图像上,求![]() 的值;
的值;
(2) 求函数![]() 的解析式;
的解析式;
(3) 当![]() 时,试探求一个函数
时,试探求一个函数![]() 使得
使得![]() 在限定定义域为
在限定定义域为
![]() 时有最小值而没有最大值.
时有最小值而没有最大值.
同下
解析:
(1)当点![]() 坐标为(
坐标为(![]() ),点
),点![]() 的坐标为
的坐标为![]() ,…………2分
,…………2分
∵点![]() 也在
也在![]() 的图像上,∴
的图像上,∴![]() ,即
,即![]() .……5分
.……5分
(根据函数![]() 的单调性求得
的单调性求得![]() ,请相应给分)
,请相应给分)
(2)设![]() 在
在![]() 的图像上
的图像上
则 ,即
,即![]() ……………………………………8分
……………………………………8分
而![]() 在
在![]() 的图像上,∴
的图像上,∴![]()
代入得,![]() 为所求.…………………………………11分
为所求.…………………………………11分
(3)![]() ;或
;或 等. …………………15分
等. …………………15分
如:当![]() 时,
时,
![]()
![]()
![]()
∵![]() 在
在![]() 单调递减, ∴
单调递减, ∴![]() 故
故 ![]() ,
,
即![]() 有最小值
有最小值![]() ,但没有最大值.………………………18分
,但没有最大值.………………………18分
(其他答案请相应给分)

练习册系列答案
相关题目
 ,当点 (x,y)
是函数y = f (x) 图象上的点时,点
,当点 (x,y)
是函数y = f (x) 图象上的点时,点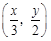 是函数y =
g(x) 图象上的点.
是函数y =
g(x) 图象上的点.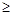 0时,求x的取值范围;
0时,求x的取值范围;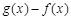 的最大值.
的最大值.