题目内容
【题目】若正实数a，b满足 
+ 
= 
，则ab+a+b的最小值为 ．
【答案】6 
+14
【解析】解：∵ 
+ 
= 
，∴3（a+1）+3（b+2）=（a+1）（b+2），
∴ab=a+2b+7，
a= 
，∵a，b都是正数，∴b＞1．
∴ab+a+b=a+2b+7+a+b=2a+3b+7= 
+3b+7
= 
=3（b﹣1）+ 
+14≥2 
+14=6 
+14．
当且仅当3（b﹣1）= 即b= +1时取等号，此时a=2+ 
．
所以答案是：6 +14．
【考点精析】利用函数的最值及其几何意义对题目进行判断即可得到答案，需要熟知利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．
练习册系列答案
相关题目
【题目】为了检测某种产品的质量（单位：千克），抽取了一个容量为N的样本，整理得到的数据作出了频率分布表和频率分布直方图如图：
分组 | 频数 | 频率 |
[17.5，20） | 10 | 0.05 |
[20，225） | 50 | 0.25 |
[22.5，25） | a | b |
[25，27.5） | 40 | c |
[27.5，30] | 20 | 0.10 |
合计 | N | 1 |
（Ⅰ）求出表中N及a，b，c的值；
（Ⅱ）求频率分布直方图中d的值；
（Ⅲ）从该产品中随机抽取一件，试估计这件产品的质量少于25千克的概率．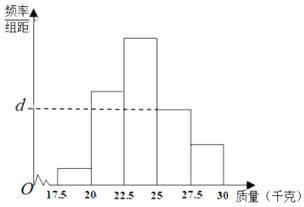
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）+B，A＞0，ω＞0，|φ|＜ 
在某一个周期的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin（ωx+φ）+B | 0 |
| 0 | ﹣ | 0 |
（1）请求出上表中的x1 ， x2 ， x3 ， 并直接写出函数f（x）的解析式；
（2）若3sin2 
﹣ 
mf（ 
﹣ 
）≥m+2对任意x∈[0，2π]恒成立，求实数m的取值范围．
