题目内容
已知等比数列{an}和等差数列{bn}均是首项为2,各项为正数的数列,且b2=4a2,a2b3=6.
(1)求数列{an}、{bn}的通项公式;
(2)求使abn<0.001成立的正整数n的最小值.
解:(1)设{an}的公比为q,{bn}的公差为d,
 ∴an=
∴an= n-2,bn=2n.
n-2,bn=2n.
(2)由(1)得abn=a2n= 2n-2,
2n-2,
∵abn<0.001,即 2n-2<0.001,
2n-2<0.001,
∴22n-2>1 000,
∴2n-2≥10,即n≥6,
∴满足题意的正整数n的最小值为6.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目

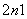 =anan+2”的( )
=anan+2”的( )
 B.
B. C.
C. D.
D.
 ,
, ,且
,且 ,则向量
,则向量 与
与 夹角的大小为( )
夹角的大小为( ) B.
B.  C.
C. D.
D.
 的定义域是( )
的定义域是( ) B.
B. C.
C. D.
D.
 <
< <0,给出下面四个不等式:①|a|>|b|;②a<b;③a+b<ab;④a3>b3.其中不正确的不等式的个数是( )
<0,给出下面四个不等式:①|a|>|b|;②a<b;③a+b<ab;④a3>b3.其中不正确的不等式的个数是( )