题目内容
已知函数y=f(x)的导函数f′(x)=3x2-2x-1,f(0)=1
(1)求y=f(x)的解析式;
(2)求函数y=f(x)在[-1,2]上的最大值和最小值.
(1)求y=f(x)的解析式;
(2)求函数y=f(x)在[-1,2]上的最大值和最小值.
考点:利用导数求闭区间上函数的最值,导数的运算,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)由题意设f(x)=x3-x2-x+a,由f(0)=1,示出f(x)=x3-x2-x+1.
(2)当f′(x)>0时,x<-
,或x>1,当f′(x)<0时,-
<x<1,由此利用导数性质能求出函数y=f(x)在[-1,2]上的最大值和最小值.
(2)当f′(x)>0时,x<-
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:(1)∵f′(x)=3x2-2x-1,
∴设f(x)=x3-x2-x+a,…(3分)
∵f(0)=1,∴a=1,∴f(x)=x3-x2-x+1.…(6分)
(2)当f′(x)>0时,x<-
,或x>1,
当f′(x)<0时,-
<x<1,
∴f(x)在区间(-1,-
),(1,2)内单调递增,在(-
,1)内单调递减…(9分)
∴f(x)极大值=f(-
)=
,f(x)极小值=f(1)=0,
又f(-1)=0,f(2)=3,
∴f(x)在[-1,2]上的最大值为f(2)=3,最小值为f(-1)=f(1)=0.…(12分)
∴设f(x)=x3-x2-x+a,…(3分)
∵f(0)=1,∴a=1,∴f(x)=x3-x2-x+1.…(6分)
(2)当f′(x)>0时,x<-
| 1 |
| 3 |
当f′(x)<0时,-
| 1 |
| 3 |
∴f(x)在区间(-1,-
| 1 |
| 3 |
| 1 |
| 3 |
∴f(x)极大值=f(-
| 1 |
| 3 |
| 32 |
| 27 |
又f(-1)=0,f(2)=3,
∴f(x)在[-1,2]上的最大值为f(2)=3,最小值为f(-1)=f(1)=0.…(12分)
点评:本题主要考查函数与导数等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、数形结合思想、函数与方程思想、化归与转化思想等.

练习册系列答案
相关题目
已知集合M={y|y>1},N={y|y=x2,x∈R},则M∩N=( )
| A、(0,+∞) |
| B、[0,+∞) |
| C、(1,+∞) |
| D、[1,+∞) |
 为了绿化城市,准备在如图所示的区域DFEBC内修建一个矩形PQRC的草坪,并建立如图平面直角坐标系,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m.
为了绿化城市,准备在如图所示的区域DFEBC内修建一个矩形PQRC的草坪,并建立如图平面直角坐标系,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m.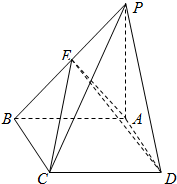 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,且PA=AB=1,F为PB中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,且PA=AB=1,F为PB中点.