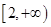题目内容
下列函数中,在其定义域内既是减函数又是奇函数为( )
A.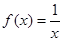 | B. |
C. | D. |
C
解析试题分析:A.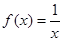 在
在 都是单调递减的,但不能说在定义域内是单调递减的;
都是单调递减的,但不能说在定义域内是单调递减的;
B. 定义域为
定义域为 ,所以是非奇非偶函数;
,所以是非奇非偶函数;
C.因为 在R上单调递减,
在R上单调递减, 在R上单调递减,所以
在R上单调递减,所以 在R上单调递减。又
在R上单调递减。又 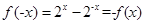 ,所以为奇函数;
,所以为奇函数;
D. 在每个单调区间上都是单调递减的,但不能说在定义域内是单调递减的。
在每个单调区间上都是单调递减的,但不能说在定义域内是单调递减的。
考点:函数的单调性;函数的奇偶性。
点评:此题是易错题,很多同学易错选A和D。我们一定要注意这种说法:在每个单调区间上都是单调递减的,但在定义域内不是单调递减的。

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
下列函数为偶函数,且在 上单调递增的函数是( )
上单调递增的函数是( )
A. | B. | C. | D. |
若函数 在
在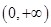 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
对于函数 ,若存在区间
,若存在区间 ,使得
,使得 ,则称区间
,则称区间 为函数
为函数 的一个“稳定区间”.现有四个函数:①
的一个“稳定区间”.现有四个函数:① ; ②
; ② ,
,
③ ④
④ .其中存在“稳定区间”的函数有( )
.其中存在“稳定区间”的函数有( )
| A.①② | B.②③ | C.③④ | D.②④ |
若函数
 的图象关于直线
的图象关于直线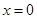 及直线
及直线 对称,且
对称,且 时,
时, ,则
,则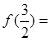 ( )
( )
A. | B. | C. | D. |
已知定义在R上的奇函数 ,满足
,满足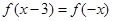 ,且在区间
,且在区间 上是增函数,若方程
上是增函数,若方程 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则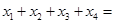
| A.6 | B. | C.18 | D.0 |
定义新运算“&”与“ ”:
”: ,
, ,则函数
,则函数
是( )
| A.奇函数 | B.偶函数 |
| C.非奇非偶函数 | D.既是奇函数又是偶函数 |
 的图象如图1所示 , 则其导函数
的图象如图1所示 , 则其导函数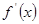 的图象大致形状是( )
的图象大致形状是( ) 
 上的任一点,若曲线在M点处的切线的倾斜角均不小于
上的任一点,若曲线在M点处的切线的倾斜角均不小于 的锐角,则实数a的取值范围是( )
的锐角,则实数a的取值范围是( )