题目内容
已知函数 的最大值不大于
的最大值不大于 ,又当
,又当 时,
时, ,则a的值为
,则a的值为
- A.1
- B.-1
- C.

- D.

A
分析:函数f(x)为开口向下的抛物线,由最大值不大于 ,列出不等式,又因为当x∈[
,列出不等式,又因为当x∈[ ,
, ]时,f(x)≥
]时,f(x)≥ ,求出在这个区间f(x)的最小值为
,求出在这个区间f(x)的最小值为 ,即可解出a的值.
,即可解出a的值.
解答:因为f(x)=- x2+ax为开口向下的抛物线,
x2+ax为开口向下的抛物线,
当x= 时,函数的最大值为
时,函数的最大值为 ,
,
由函数的最大值不大于 ,列出不等式为:
,列出不等式为:
 ≤
≤ ,解得-1≤a≤1;
,解得-1≤a≤1;
因为当x∈[ ,
, ]时,f(x)≥
]时,f(x)≥ ,
,
即在此区间f(x)的最小值为 ,
,
而即f( )=
)= -
- =
= ,解得a=1,f(
,解得a=1,f( )=
)= -
-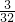 =
= ,
,
解得a= >1舍去.所以a=1.
>1舍去.所以a=1.
故选A.
点评:本题考查学生理解函数恒成立的条件以及会求二次函数最值的能力,解题时要认真审题,注意等价转化思想的合理运用.
分析:函数f(x)为开口向下的抛物线,由最大值不大于
 ,列出不等式,又因为当x∈[
,列出不等式,又因为当x∈[ ,
, ]时,f(x)≥
]时,f(x)≥ ,求出在这个区间f(x)的最小值为
,求出在这个区间f(x)的最小值为 ,即可解出a的值.
,即可解出a的值.解答:因为f(x)=-
 x2+ax为开口向下的抛物线,
x2+ax为开口向下的抛物线,当x=
 时,函数的最大值为
时,函数的最大值为 ,
,由函数的最大值不大于
 ,列出不等式为:
,列出不等式为: ≤
≤ ,解得-1≤a≤1;
,解得-1≤a≤1;因为当x∈[
 ,
, ]时,f(x)≥
]时,f(x)≥ ,
,即在此区间f(x)的最小值为
 ,
,而即f(
 )=
)= -
- =
= ,解得a=1,f(
,解得a=1,f( )=
)= -
-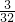 =
= ,
,解得a=
 >1舍去.所以a=1.
>1舍去.所以a=1.故选A.
点评:本题考查学生理解函数恒成立的条件以及会求二次函数最值的能力,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 的最大值不大于
的最大值不大于 ,又当
,又当
 .证明
.证明
 的最大值不大于
的最大值不大于 ,又当
,又当 时,
时, ,则a= .
,则a= .