题目内容
已知函数![]() 的最大值不大于
的最大值不大于![]() ,又当
,又当![]()
(1)求a的值;
(2)设![]()
(1)解:由于![]() 的最大值不大于
的最大值不大于![]() 所以
所以
![]() ① ………………3分
① ………………3分
又![]() 所以
所以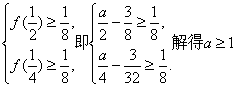 . ②
. ②
由①②得![]() ………………6分
………………6分
(2)证法一:(i)当n=1时,![]() ,不等式
,不等式![]() 成立;
成立;
因![]() 时不等式也成立.
时不等式也成立.
(ii)假设![]() 时,不等式
时,不等式![]() 成立,因为
成立,因为![]() 的
的
对称轴为![]() 知
知![]() 为增函数,所以由
为增函数,所以由![]() 得
得
![]() ………………8分
………………8分
于是有
![]()
…………12分
所以当n=k+1时,不等式也成立.
根据(i)(ii)可知,对任何![]() ,不等式
,不等式![]() 成立.…………14分
成立.…………14分
证法二:(i)当n=1时,![]() ,不等式
,不等式![]() 成立;
成立;
(ii)假设![]() 时不等式成立,即
时不等式成立,即![]() ,则当n=k+1时,
,则当n=k+1时,
![]() ………………8分
………………8分
因![]() 所以
所以
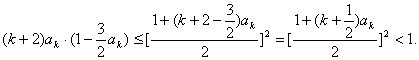 ……12分
……12分
于是![]() 因此当n=k+1时,不等式也成立.
因此当n=k+1时,不等式也成立.
根据(i)(ii)可知,对任何![]() ,不等式
,不等式![]() 成立.…………14分
成立.…………14分

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 的最大值不大于
的最大值不大于 ,又当
,又当
 .证明
.证明
 的最大值不大于
的最大值不大于 ,又当
,又当 时,
时, ,则a= .
,则a= .