题目内容
(本小题满分10分)在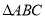 中,内角
中,内角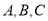 所对的边分别为
所对的边分别为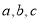 ,若
,若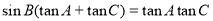 .
.
(1)求证: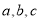 成等比数列;(2)若
成等比数列;(2)若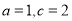 ,求
,求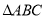 的面积
的面积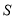 .
.
(1)见解析,(2)
【解析】
试题分析:(1)第一步首先利用切化弦,整理后的正弦式借助正弦定理进行角化边即可得出结论,第二步借助第一步结论,把 代入得:
代入得: ,利用余弦定理求出
,利用余弦定理求出
 ,最后求面积.
,最后求面积.
试题解析:(1)由已知 .得:
.得: ,
,
即: ,即:
,即:
由正弦定理: ,所以:
,所以: 成等比数列.
成等比数列.
(2)由(1)知: ,
, ,所以:
,所以: ,
,
由余弦定理: ,所以:
,所以:
所以:
考点:1.三角函数的切化弦;2.正弦定理;3.余弦定理;4.三角形的面积公式;
考点分析: 考点1:解三角形 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
 ;
; .
. ,若
,若 ,则实数
,则实数 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 的等边
的等边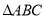 中,
中,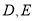 分别在边BC与AC上,且
分别在边BC与AC上,且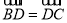 ,
,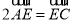
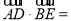 ( )
( )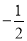 B.
B. 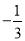 C.
C.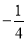 D.
D.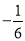
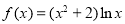 ,
,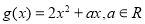
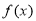 是
是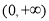 上的增函数;
上的增函数;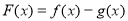 ,当
,当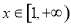 时,
时,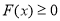 恒成立,求
恒成立,求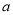 的取值范围.
的取值范围. ,若方程
,若方程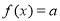 有四个不同的解
有四个不同的解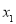 ,
,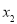 ,
, ,
,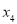 ,且
,且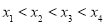 ,则
,则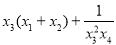 的取值范围是( )
的取值范围是( )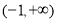 B.
B.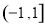 C.
C.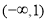 D.
D.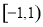
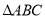 中“
中“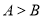 ”是“
”是“ ”的( )
”的( )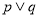 为真命题,则
为真命题,则 为真命题
为真命题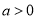 ,
,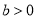 ”是“
”是“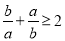 ”的充分必要条件
”的充分必要条件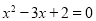 ,则
,则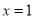 或
或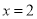 ”的逆否命题为“若
”的逆否命题为“若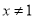 或
或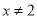 ,则
,则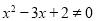 ”
”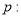
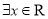 ,使得
,使得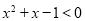 ,则
,则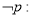
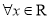 ,使得
,使得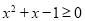
 ,
, ,则
,则 .
.