题目内容
(本小题满分10分)如图,圆周角 的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.

(Ⅰ)求证: ;
;
(Ⅱ)若D,E,C,F四点共圆,且弧长AC等于弧长BC,求 .
.
(1)证明详见解析;(2)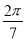 .
.
【解析】
试题分析:本题主要考查几何证明、四点共圆、角的转化等基础知识,意在考查考生的分析问题解决问题的能力、读图能力、运算求解能力.第一问,利用圆的弦切角相等,同弧所对的圆周角相等,角平分线进行角间的转化,得到内错角相等,即得证BC∥DE;第二问,结合第一问中的结论,得∠CFA=∠ACF,利用同弧所对圆周角相等得∠CBA=∠BAC,通过角之间的转化,在三角形ACF中,计算出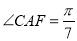 ,从而得到
,从而得到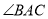 的值.
的值.
试题解析:(Ⅰ)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,
所以∠EDC=∠DCB,
所以BC∥DE. 4分
(Ⅱ)【解析】
因为D,E,C,F四点共圆,所以
∠CFA=∠CED,由(Ⅰ)知∠ACF=∠CED,所以
∠CFA=∠ACF.设∠DAC=∠DAB=x,
因为弧长AC=弧长BC,所以∠CBA=∠BAC=2x,
所以∠CFA=∠FBA+∠FAB=3x,
在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,则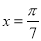 ,
,
所以∠BAC=2x=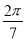 . 10分
. 10分
考点:几何证明、四点共圆、角的转化.
考点分析: 考点1:几何证明选讲 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
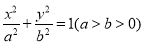 过点
过点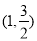 ,且椭圆C的离心率为
,且椭圆C的离心率为 .
.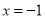 上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线
上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线 .证明:直线
.证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标. 的值域为( )
的值域为( ) B.
B. C.
C. D.
D.
 ,则抛物线的标准方程是( )
,则抛物线的标准方程是( ) B.
B. C.
C. D.
D.
 的前n项和为
的前n项和为 ,满足
,满足 ,且
,且 .
. 成等差数列,求证:
成等差数列,求证: 成等差数列.
成等差数列.
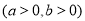 的右焦点,过点F向C的一条渐近线引垂直,垂足为A,交另一条渐近线于点B,若
的右焦点,过点F向C的一条渐近线引垂直,垂足为A,交另一条渐近线于点B,若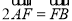 ,则C的离心率是( )
,则C的离心率是( )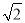 B.
B.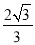 C.2 D.
C.2 D.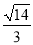
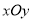 中,曲线
中,曲线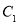 和
和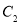 的参数方程分别为
的参数方程分别为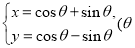 为参数
为参数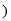 和
和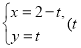 为参数
为参数 .以原点
.以原点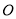 为极点,
为极点,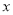 轴正半轴为极轴,建立极坐标系,则曲线
轴正半轴为极轴,建立极坐标系,则曲线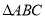 中,内角
中,内角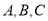 所对的边分别为
所对的边分别为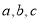 ,若
,若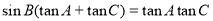 .
.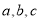 成等比数列;(2)若
成等比数列;(2)若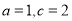 ,求
,求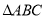 的面积
的面积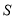 .
.