题目内容
(本小题满分14分)设函数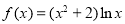 ,
,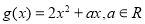
(1)证明: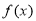 是
是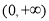 上的增函数;
上的增函数;
(2)设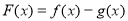 ,当
,当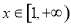 时,
时,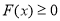 恒成立,求
恒成立,求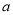 的取值范围.
的取值范围.
(1)见解析;(2)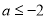
【解析】
试题分析:第一步证明函数 是
是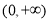 上的增函数,只需证明)
上的增函数,只需证明)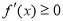 成立,若
成立,若
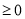 ,我们只需
,我们只需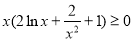 ,由于
,由于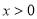 ,令
,令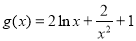 ,因为
,因为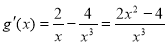 ,所以:
,所以: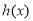 在
在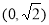 上递减,
上递减, 上递增,
上递增,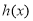 最小值
最小值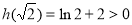 故:
故: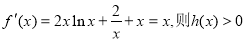 ,所以:
,所以: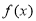 是
是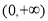 上的增函数.
上的增函数.
(2)第二步求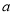 的取值范围,可分离常数
的取值范围,可分离常数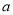 ,,由
,,由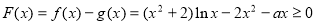 得:
得:
 在
在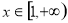 上恒成立,只需求出
上恒成立,只需求出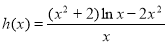 的最小值即可.
的最小值即可.
试题解析:(1)若证明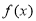 是
是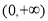 上的增函数,只需证明
上的增函数,只需证明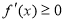 在
在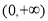 恒成立,
恒成立,
即:

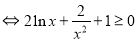
设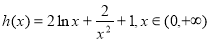 ,
,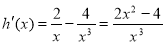
所以: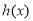 在
在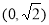 上递减,
上递减, 上递增,
上递增,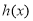 最小值
最小值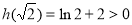
故: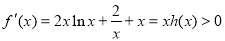 ,所以:
,所以: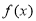 是
是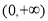 上的增函数.
上的增函数.
(2)由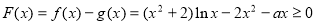 得:
得: 在
在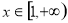 上恒成立,设
上恒成立,设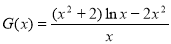 ,则
,则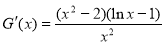 ,所以
,所以 在
在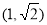 递增,
递增,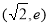 递减,
递减,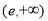 递增,所以
递增,所以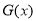 的最小值为
的最小值为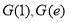 中较小的,
中较小的,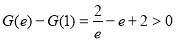 ,
,
所以: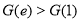 ,即:
,即: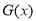 在
在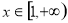 的最小值为
的最小值为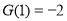 ,
,
只需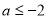
考点:1.导数与函数的单调性;2.研究一个函数的单调性与极值,3.极端原理的使用;
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 ,则抛物线的标准方程是( )
,则抛物线的标准方程是( ) B.
B. C.
C. D.
D.
 为等比数列,若
为等比数列,若 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,若方程
,若方程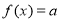 有四个不同的解
有四个不同的解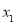 ,
,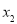 ,
,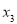 ,
,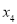 ,且
,且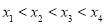 ,则
,则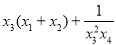 的取值范围是( )
的取值范围是( )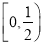 B.
B.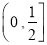 C.
C.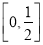 D.
D.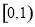
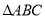 中 “
中 “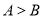 ”是“
”是“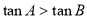 ”的( )
”的( )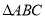 中,内角
中,内角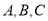 所对的边分别为
所对的边分别为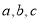 ,若
,若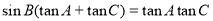 .
.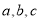 成等比数列;(2)若
成等比数列;(2)若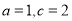 ,求
,求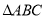 的面积
的面积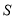 .
.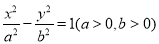 的一个焦点到一条渐近线的距离为
的一个焦点到一条渐近线的距离为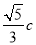 (
(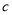 为双曲线的半焦距长),则双曲线的离心率为( )
为双曲线的半焦距长),则双曲线的离心率为( )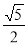 B.
B.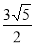 C.
C.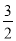 D.
D.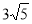
 被圆
被圆 截得的弦长为 .
截得的弦长为 .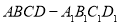 中,底面
中,底面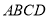 是等腰梯形,
是等腰梯形,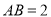 ,
,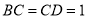
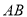 ∥
∥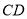 ,顶点
,顶点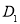 在底面
在底面 .
.
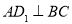 ;
;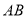 上是否存在点
上是否存在点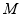 ,使得
,使得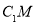 ∥平面
∥平面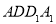 ?若存在,确定点
?若存在,确定点